Kepler's Laws

Johannes Kepler 1571-1630

Johannes Kepler was born poor and sickly in what is now Germany. His father left home when Johannes was five and never returned. It is believed he was killed in a war. While Johannes was pursuing higher education his mother was tried as a witch. Johannes hired a legal team which was able to obtain her release, mostly on legal technicalities.

Although he had an eventful life, Kepler is most remembered for "cracking the code" that describes the orbits of the planets.

Prior to Kepler's discoveries, the predominate theory of the solar system was an Earth-centered geometry as described by Ptolemy. A Sun-centered theory had been proposed by Copernicus, but its predictions were plagued with inaccuracies.

Working in Prague at the Royal Observatory of Denmark, Kepler succeeded by using the notes of his predecessor, Tycho Brahe, which recorded the precise position of Mars relative to the Sun and Earth.

Kepler developed his laws empirically from observation, as opposed to deriving them from some fundamental theoretical principles. About 30 years after Kepler died, Isaac Newton was able to derive Kepler's Laws from basic laws of gravity.




Law 1. The orbits of the planets are ellipses, with the Sun at one focus.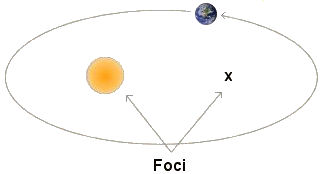

Any ellipse has two geometrical points called the foci (focus for singular). There is no physical significance of the focus without the Sun but it does have mathematical significance. The total distance from a planet to each of the foci added together is always the same regardless of where the planet is in its orbit.

The importance of this is that by not assuming the orbits are perfect circles, the accuracy of predictions in the Sun-centered theory was (for the first time) greater than those of the Earth-centered theory.




Law 2. The line joining a planet to the Sun sweeps out equal areas in equal times as the planet travels around the ellipse.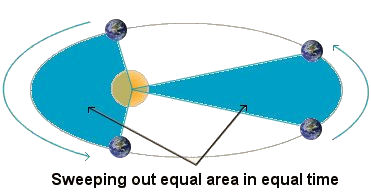



In any given amount of time, 30 days for example, the planet sweeps out the same amount of area regardless of which 30 day period you choose. Therefore the planet moves faster when it is nearer the Sun and slower when it is farther from the Sun. A planet moves with constantly changing speed as it moves about its orbit. The fastest a planet moves is at perihelion (closest) and the slowest is at aphelion (farthest).




Law 3. The square of the total time period (T) of the orbit is proportional to the cube of the average distance of the planet to the Sun (R).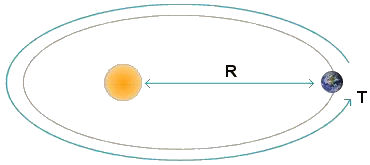



This law is sometimes referred to as the law of harmonies. It compares the orbital time period and radius of an orbit of any planet, to those of the other planets. The discovery Kepler made is that the ratio of the squares of the revolutionary time periods to the cubes of the average distances from the Sun, is the same for every planet.