- Problem 1. Solve the PDE \begin{equation*} \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0 \end{equation*} subject to the boundary conditions \begin{alignat}{2} u(x,0) & = 0, & \qquad u(x,L) & = 0, \qquad 0 \leq x \leq K, \\ u(0,y) & = g_1(y), & \qquad u(K,y) & = g_2(y), \qquad 0 \leq y \leq L. \\ \end{alignat}
- Problem 2. Solve the PDE \begin{equation*} \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0. \end{equation*} subject to the boundary conditions \begin{alignat}{2} u(x,0) & = f_1(x), & \qquad u(x,L) & = f_2(x), \qquad 0 \leq x \leq K, \\ u(0,y) & = 0, & \qquad u(K,y) & = 0, \qquad 0 \leq y \leq L. \\ \end{alignat}
- First we use separation of variables to find a "few" solutions of the homogeneous problem: \begin{equation} \label{eqHBVP} \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0, \quad u(x,0) = 0, \quad u(x,L) = 0, \quad 0 \leq x \leq K. \end{equation}
- Substituting $u(x,y) = A(x)B(y)$ in PDE yields \[ A^{\prime\prime}(x) B(y) + A(x) B^{\prime\prime}(y) = 0. \] Separating variables further yields \[ \frac{A^{\prime\prime}(x)}{A(x)} = - \frac{B^{\prime\prime}(y)}{B(y)} = \lambda \] where $\lambda$ is a constant to be determined.
- The last expression leads to two ordinary differential equations \[ A^{\prime\prime}(x) = \lambda A(x), \qquad - B^{\prime\prime}(y) = \lambda B(y). \] Further, the boundary conditions \begin{equation*} A(x)B(0) = 0, \qquad A(x)B(L) = 0, \qquad 0 \leq x \leq K, \end{equation*} yield the boundary conditions for $B$: $B(0) = 0, \quad B(L) = 0$.
- Thus we have to solve two ordinary differential equations problems. The first one is an eigenvalue problem for $B$ \begin{equation} \label{eqEBVB} - B^{\prime\prime}(y) = \lambda B(y), \qquad B(0) = 0, \quad B(L) = 0. \end{equation} The second one is just an ODE involving $A$: \begin{equation} \label{eqODEA} A^{\prime\prime}(x) = \lambda A(x). \end{equation}
- We have solved the eigenvalue problem \eqref{eqEBVB} earlier. The solutions are \begin{equation} \label{eqEBVBs} \lambda_n = \left( \frac{n \pi}{L} \right)^2, \qquad \sin\left( \frac{n \pi}{L} y \right), \qquad n \in {\mathbb N}. \end{equation}
- With $\lambda$-s from \eqref{eqEBVBs} we solve the ODE \eqref{eqODEA}. A popular fundamental set of solutions of \eqref{eqODEA} is \[ \cosh\left( \frac{n \pi}{L} x \right), \qquad \sinh\left( \frac{n \pi}{L} x \right), \qquad n \in {\mathbb N}. \] However, since the important values for $x$ are $0$ and $K$ we will choose the following fundamental set of solutions of \eqref{eqODEA}: \begin{equation} \label{eqODEAs} \dfrac{\sinh\left( \dfrac{n \pi}{L} (K- x) \right)}{\sinh\left( \dfrac{n \pi}{L} K \right)}, \qquad \frac{\sinh\left( \dfrac{n \pi}{L} x \right)}{\sinh\left( \dfrac{n \pi}{L} K \right)}, \qquad n \in {\mathbb N}. \end{equation} Why do we choose these solutions? We choose these solutions since they take nice values at $0$ and at $K$. The value of the first solution at $0$ is $1$ and at $K$ is $0$. The value of the second solution at $0$ is $0$ and at $K$ is $1$. There are no better solutions for our task.
- Finally we have a "few" solutions of \eqref{eqHBVP}: \begin{equation} \label{eqHBVPs} \sin\left( \dfrac{n \pi}{L} y \right)\dfrac{\sinh\left( \dfrac{n \pi}{L} (K- x) \right)}{\sinh\left( \dfrac{n \pi}{L} K \right)}, \qquad \sin\left( \frac{n \pi}{L} y \right)\, \dfrac{\sinh\left( \dfrac{n \pi}{L} x \right)}{\sinh\left( \dfrac{n \pi}{L} K \right)}, \qquad n \in {\mathbb N}. \end{equation}
- By the superposition principle, for arbitrary $a_n$ and $b_n$ the function \begin{equation} \label{eqBVPs} u_1(x,y) = \sum_{n=1}^{\infty} a_n \sin\left( \dfrac{n \pi}{L} y \right)\dfrac{\sinh\left( \dfrac{n \pi}{L} (K- x) \right)}{\sinh\left( \dfrac{n \pi}{L} K \right)} + \sum_{n=1}^{\infty} b_n \sin\left( \frac{n \pi}{L} y \right)\, \dfrac{\sinh\left( \dfrac{n \pi}{L} x \right)}{\sinh\left( \dfrac{n \pi}{L} K \right)} \end{equation} is also a solution of \eqref{eqHBVP}.
- Next we choose $a_n$ and $b_n$ such that $u_1(0,y) = g_1(y)$ and $u_1(K,y) = g_2(y)$. Substituting $x=0$ and $x=K$ in \eqref{eqBVPs} we get \[ \sum_{n=1}^{\infty} a_n \sin\left( \dfrac{n \pi}{L} y \right) = g_1(y) \] and \[ \sum_{n=1}^{\infty} b_n \sin\left( \frac{n \pi}{L} y \right) = g_2(y) \]
- Using the orthogonality of the sine functions in \eqref{eqEBVBs} we get \[ a_n = \frac{2}{L} \int_0^L g_1(y) \sin\left( \dfrac{n \pi}{L} y \right) dy, \qquad n \in {\mathbb N}, \] and \[ b_n = \frac{2}{L} \int_0^L g_2(y) \sin\left( \dfrac{n \pi}{L} y \right) dy, \qquad n \in {\mathbb N}. \]
- Notice that Problem 1 and Problem 2 are symmetric in the sense that the roles of $x$ and $y$ are reversed.
- Using this symmetry we can immediately read that a few solutions of the homogeneous boundary value problem \begin{equation} \label{eqHBVP2} \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0, \quad u(0,y) = 0, \quad u(K,y) = 0, \quad 0 \leq y \leq L. \end{equation} are \begin{equation} \label{eqHBVP2s} \sin\left( \dfrac{n \pi}{K} x \right)\dfrac{\sinh\left( \dfrac{n \pi}{K} (L - y) \right)}{\sinh\left( \dfrac{n \pi}{K} L \right)}, \qquad \sin\left( \frac{n \pi}{K} x \right)\, \dfrac{\sinh\left( \dfrac{n \pi}{K} y \right)}{\sinh\left( \dfrac{n \pi}{K} L \right)}, \qquad n \in {\mathbb N}. \end{equation}
- By the superposition principle, for arbitrary $c_n$ and $d_n$ the function \begin{equation} \label{eqBVP2s} u_2(x,y) = \sum_{n=1}^{\infty} c_n \sin\left( \dfrac{n \pi}{K} x \right)\dfrac{\sinh\left( \dfrac{n \pi}{K} (L - y) \right)}{\sinh\left( \dfrac{n \pi}{K} L \right)} + \sum_{n=1}^{\infty} d_n \sin\left( \frac{n \pi}{K} x \right)\, \dfrac{\sinh\left( \dfrac{n \pi}{K} y \right)}{\sinh\left( \dfrac{n \pi}{K} L \right)} \end{equation} is also a solution of \eqref{eqHBVP2}.
- Next we choose $c_n$ and $d_n$ such that $u_2(x,0) = f_1(x)$ and $u_2(x,L) = f_2(x)$. Substituting $y=0$ and $y=L$ in \eqref{eqBVP2s} we get \[ \sum_{n=1}^{\infty} c_n \sin\left( \dfrac{n \pi}{K} x \right) = f_1(x) \] and \[ \sum_{n=1}^{\infty} d_n \sin\left( \frac{n \pi}{K} x \right) = f_2(x) \]
- Using the orthogonality of the sine functions we get \[ c_n = \frac{2}{K} \int_0^K f_1(x) \sin\left( \dfrac{n \pi}{K} x \right) dx, \qquad n \in {\mathbb N}, \] and \[ d_n = \frac{2}{K} \int_0^K f_2(x) \sin\left( \dfrac{n \pi}{K} x \right) dx, \qquad n \in {\mathbb N}. \]
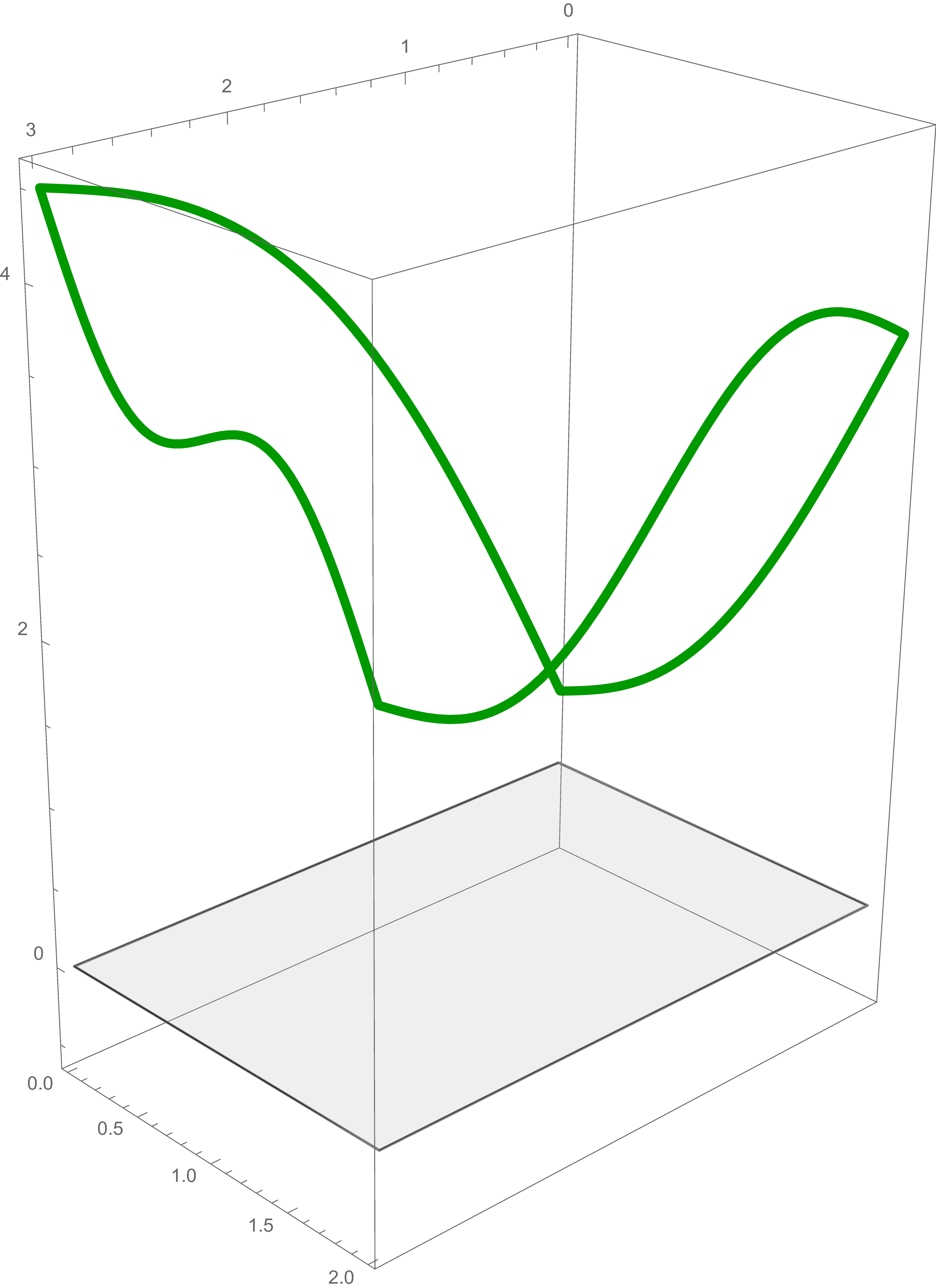
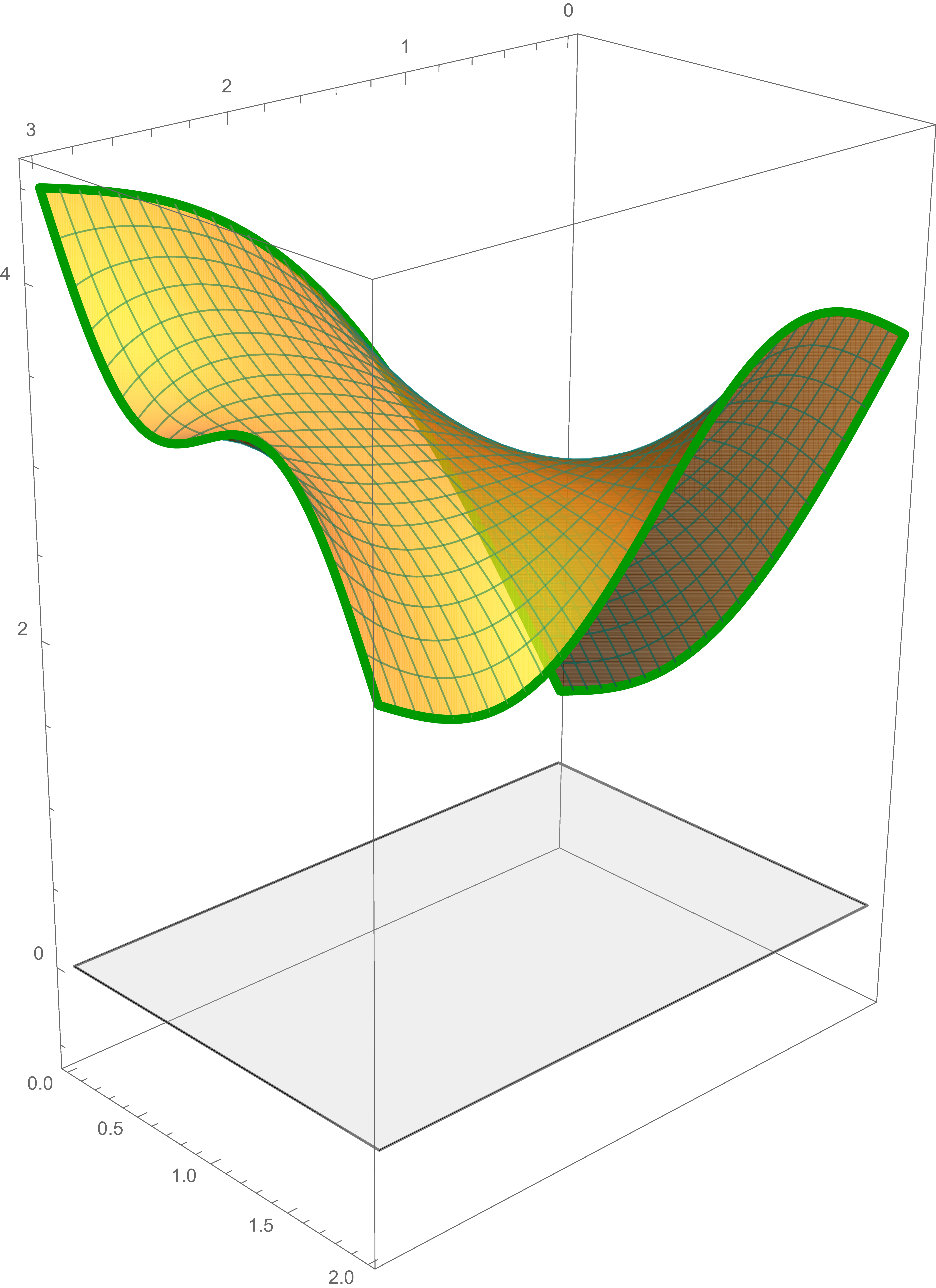
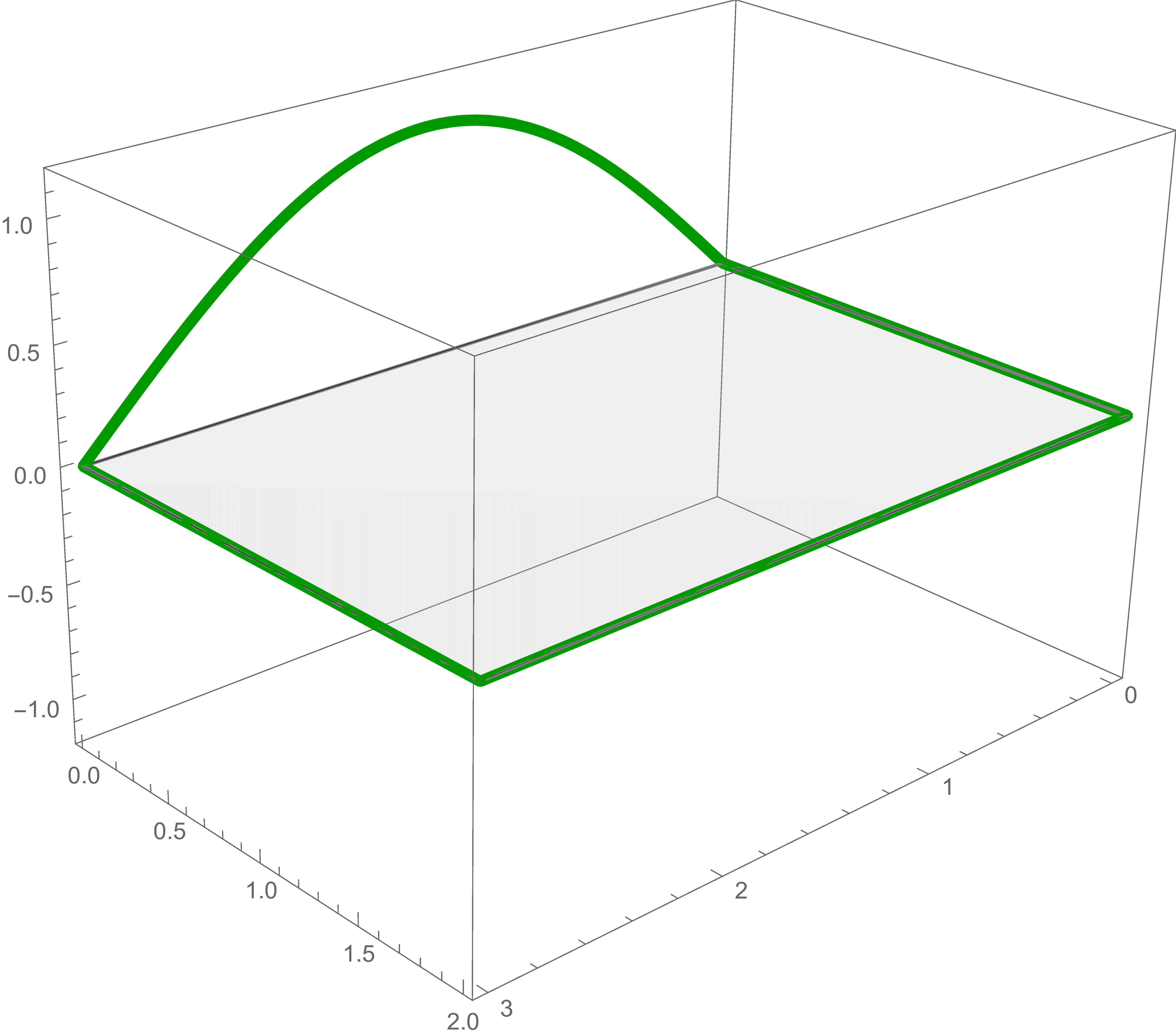
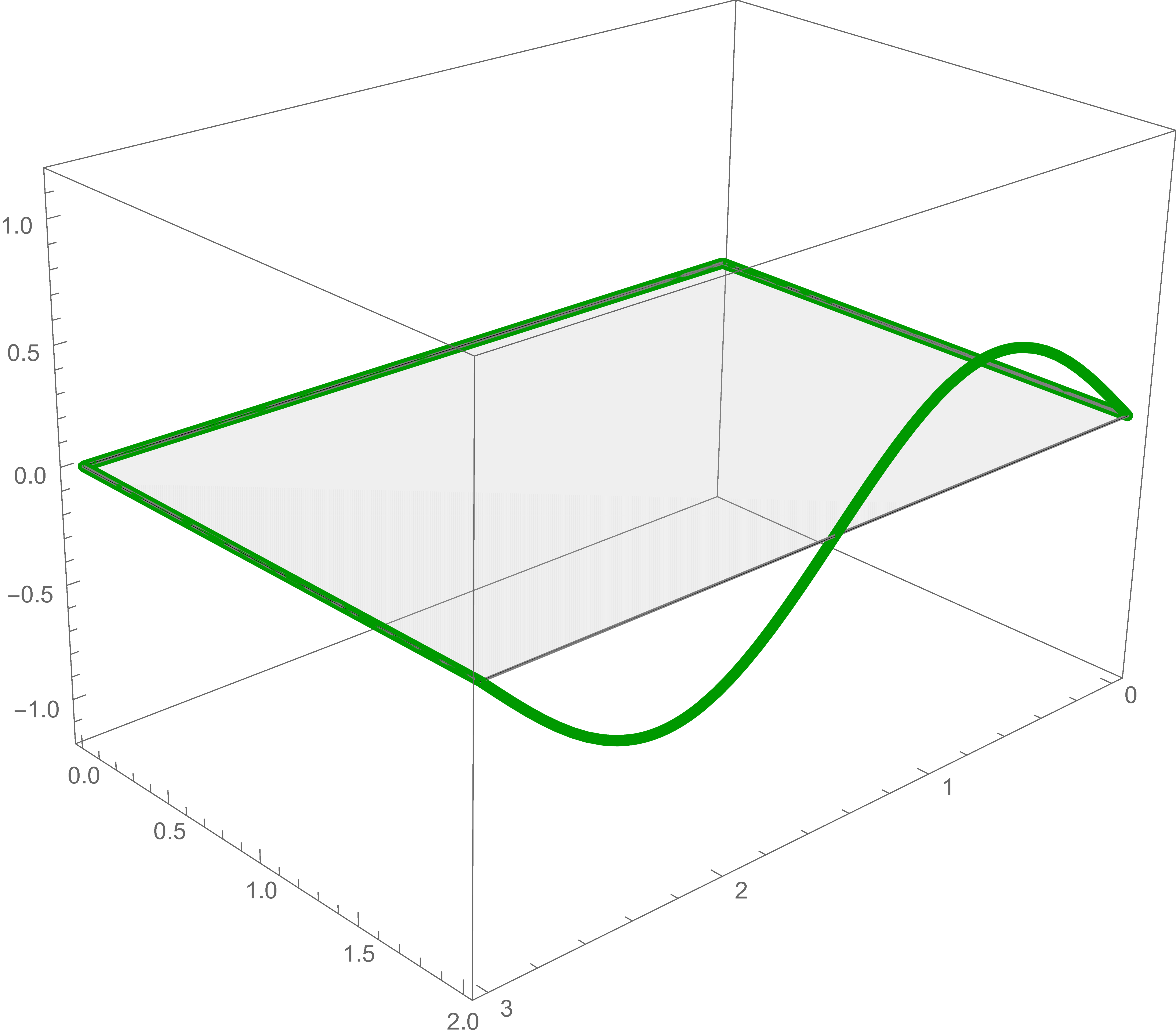
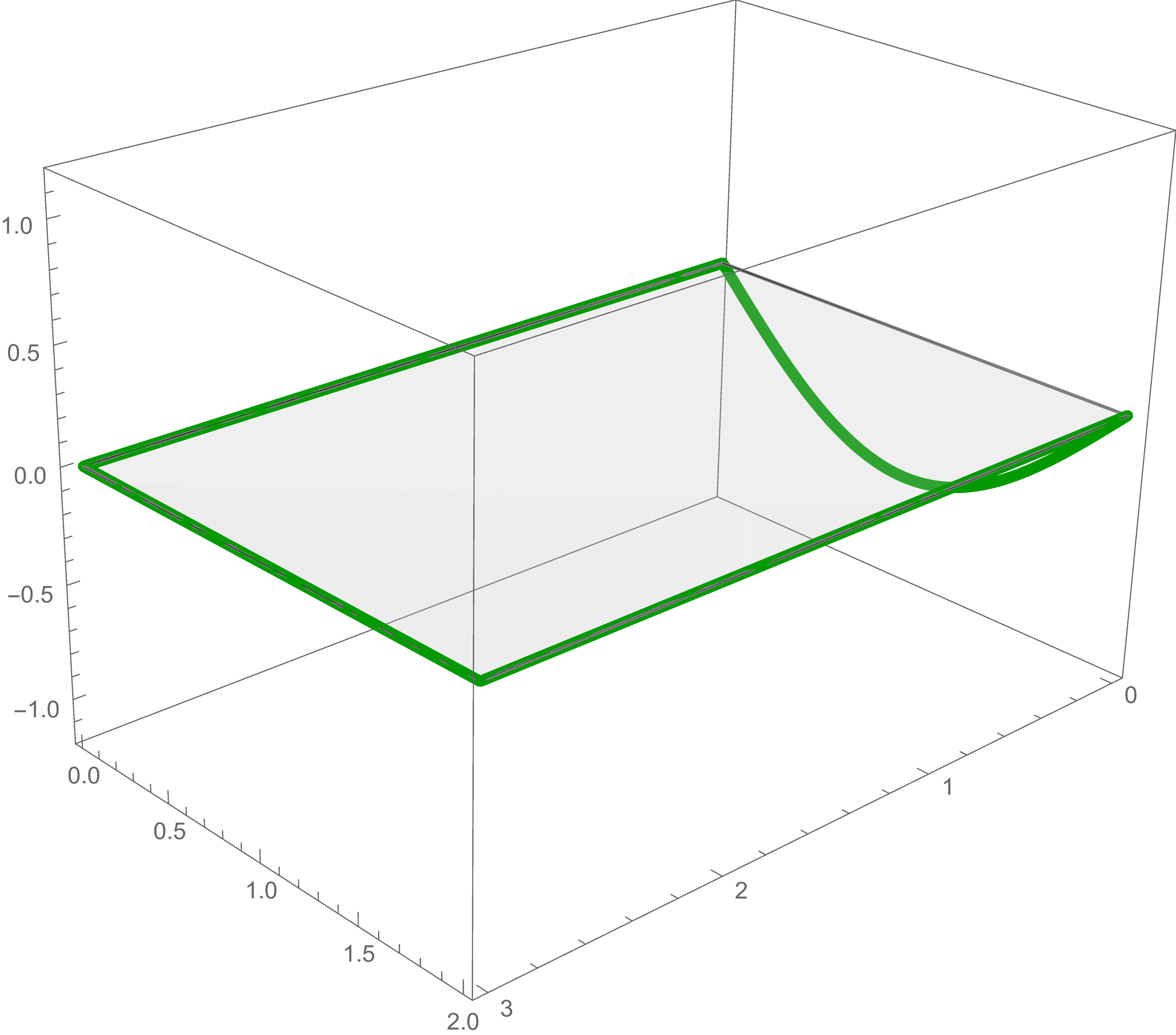
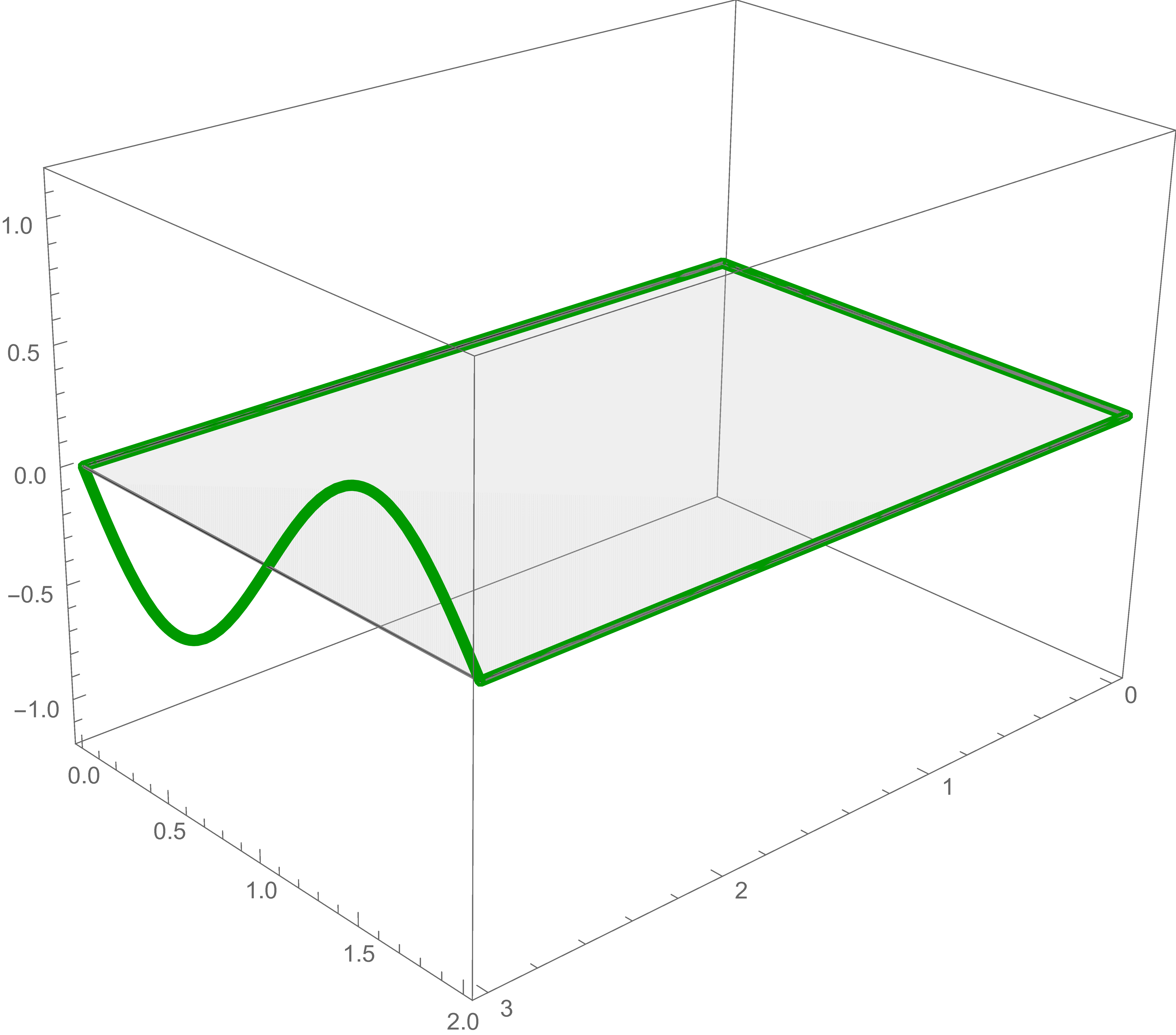
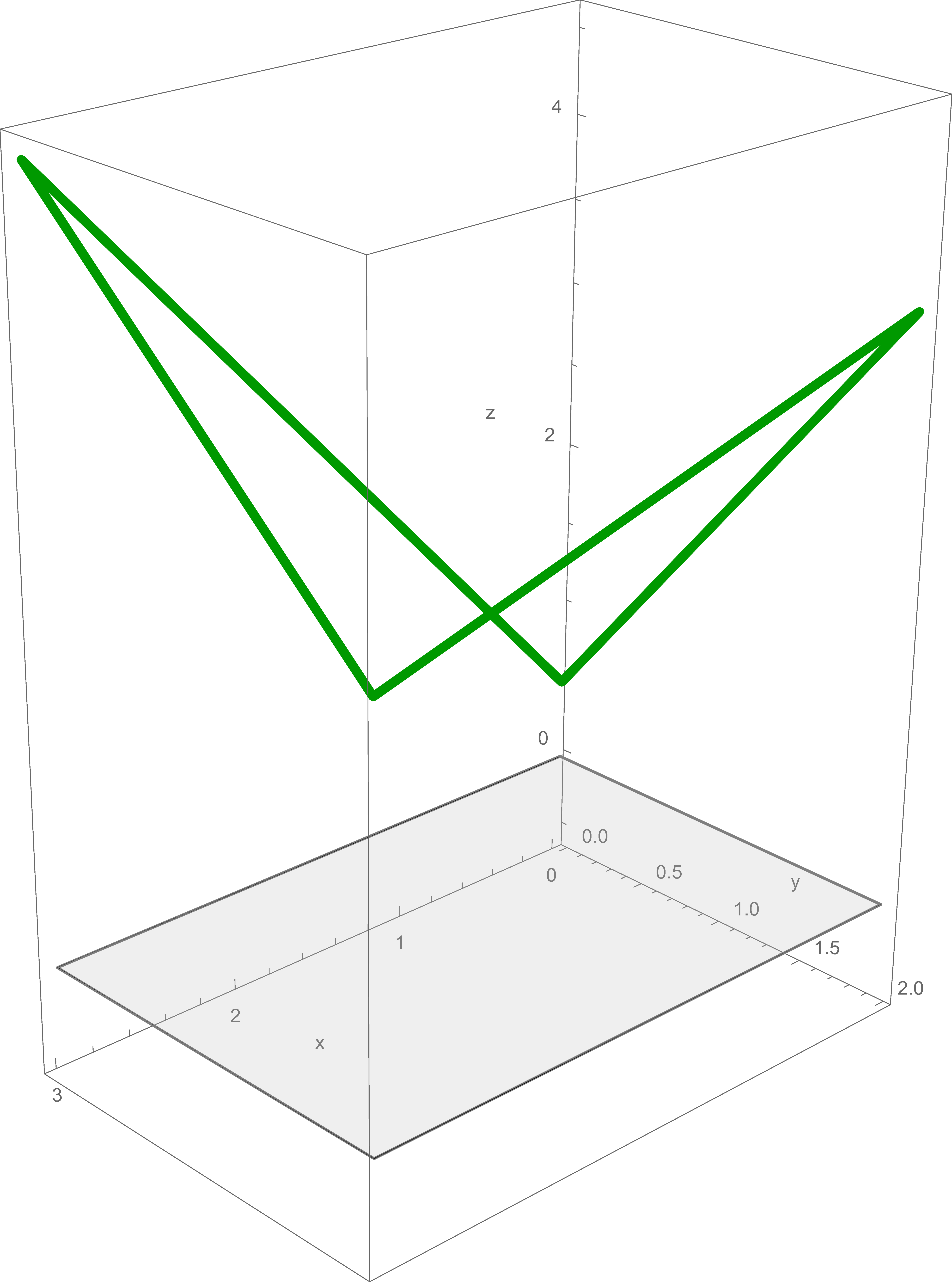
For each of these five boundary conditions we find the exact solution of Laplace's Equation and add them together to get the solution of the original problem.
The solution of Laplace's equation that satisfies the first boundary condition is \[ \sin \left(\frac{\pi}{3} x\right) \frac{\sinh \left(\frac{\pi}{3} (2-y)\right)}{\sinh\left(\frac{\pi }{3}\, 2 \right)} \]
The solution of Laplace's equation that satisfies the second boundary condition is \[ \frac{1}{2} \sin \left( \frac{2\pi}{3} x \right) \frac{\sinh \left(\frac{2\pi}{3} (2-y)\right)}{\sinh\left(\frac{2\pi }{3}\, 2 \right)} \]
The first solution, the second solution and the sum of the first and the second solutions are
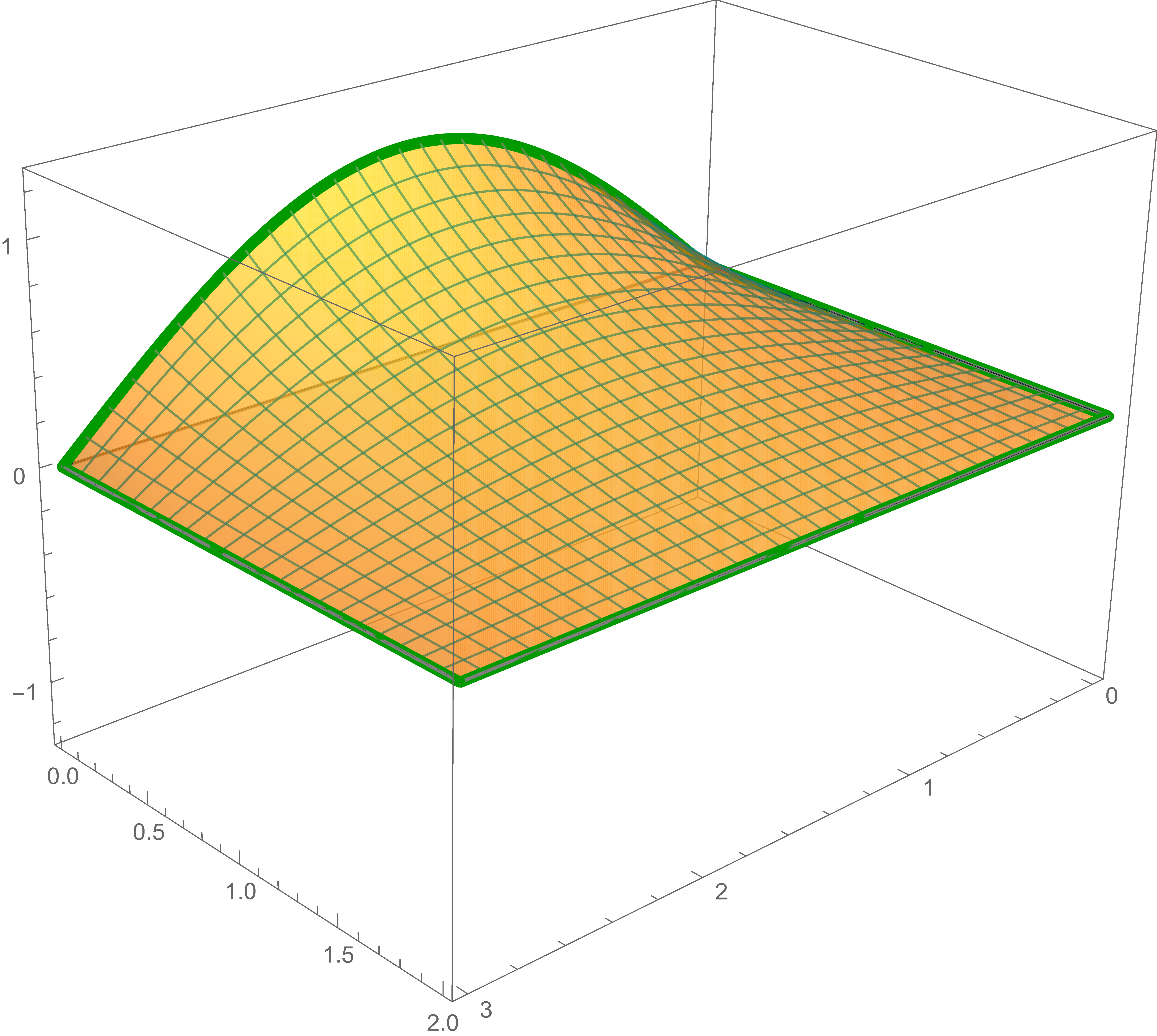
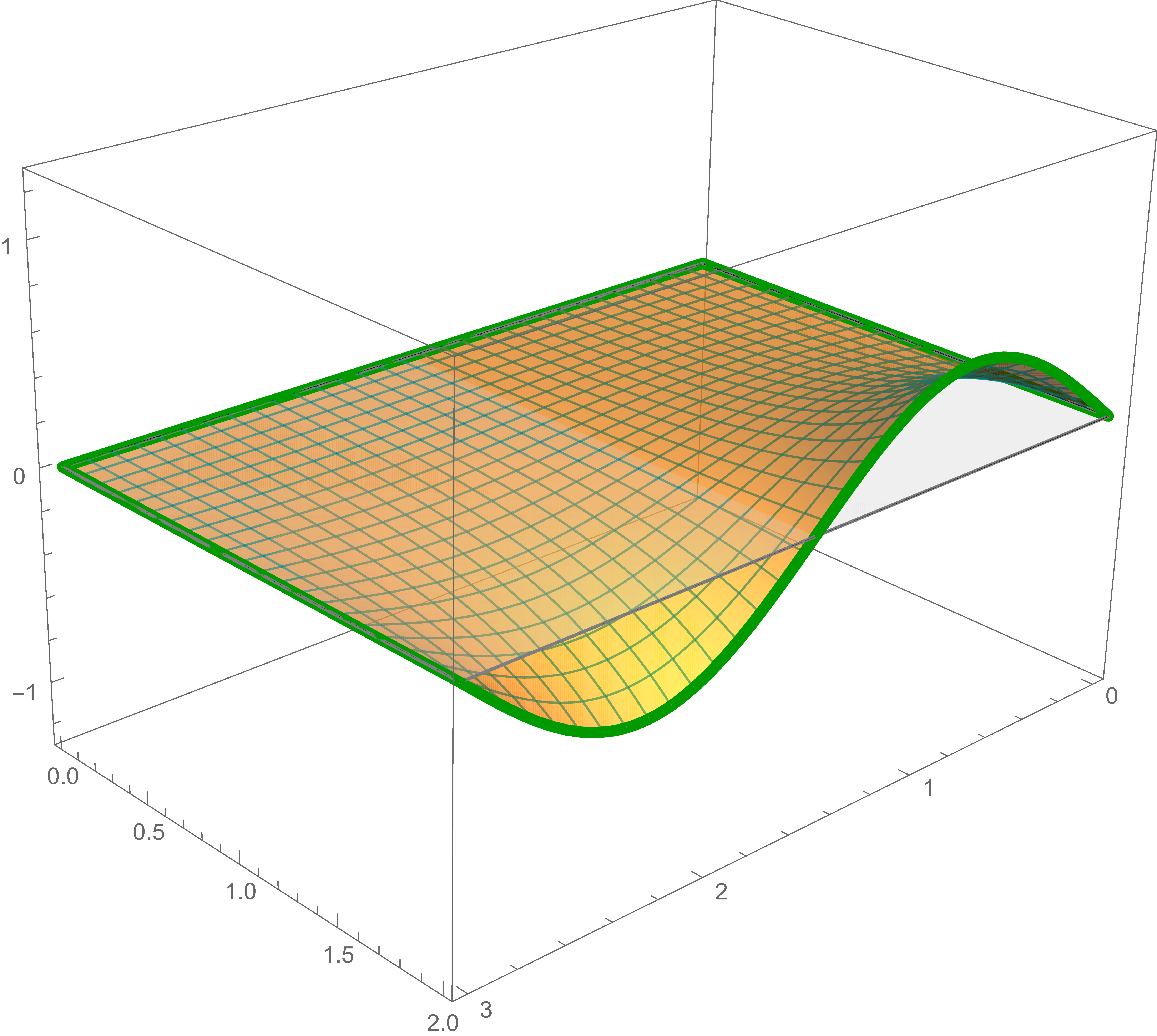
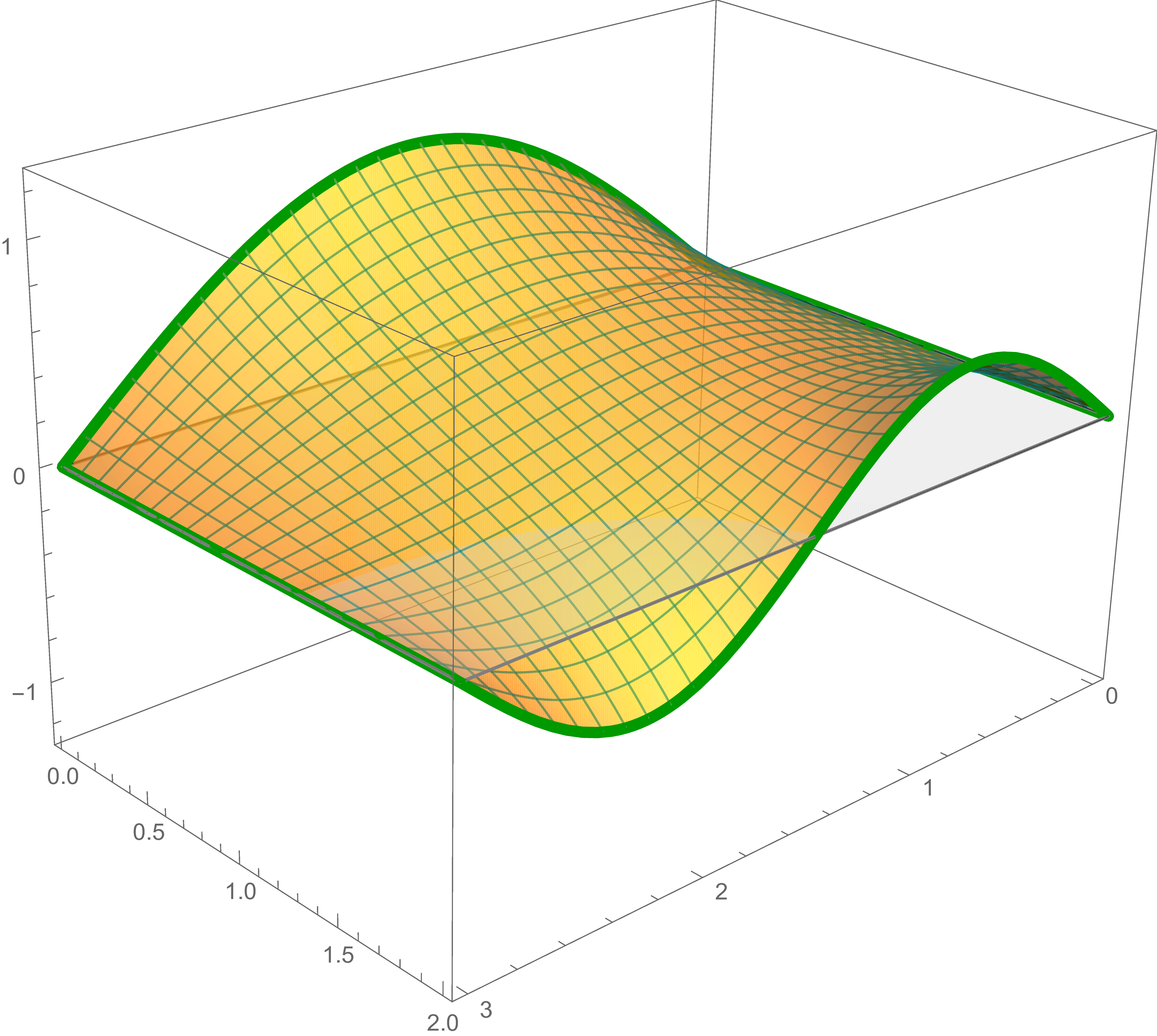
The solution of Laplace's equation that satisfies the third boundary condition is \[ -\frac{2}{3} \sin \left( \frac{\pi}{2} y \right) \frac{\sinh \left(\frac{\pi}{2} (3-x)\right)}{\sinh\left(\frac{\pi}{2}\, 3 \right)} \]
The third solution, the preceding sum and the sum of the first, the second and the third solutions are
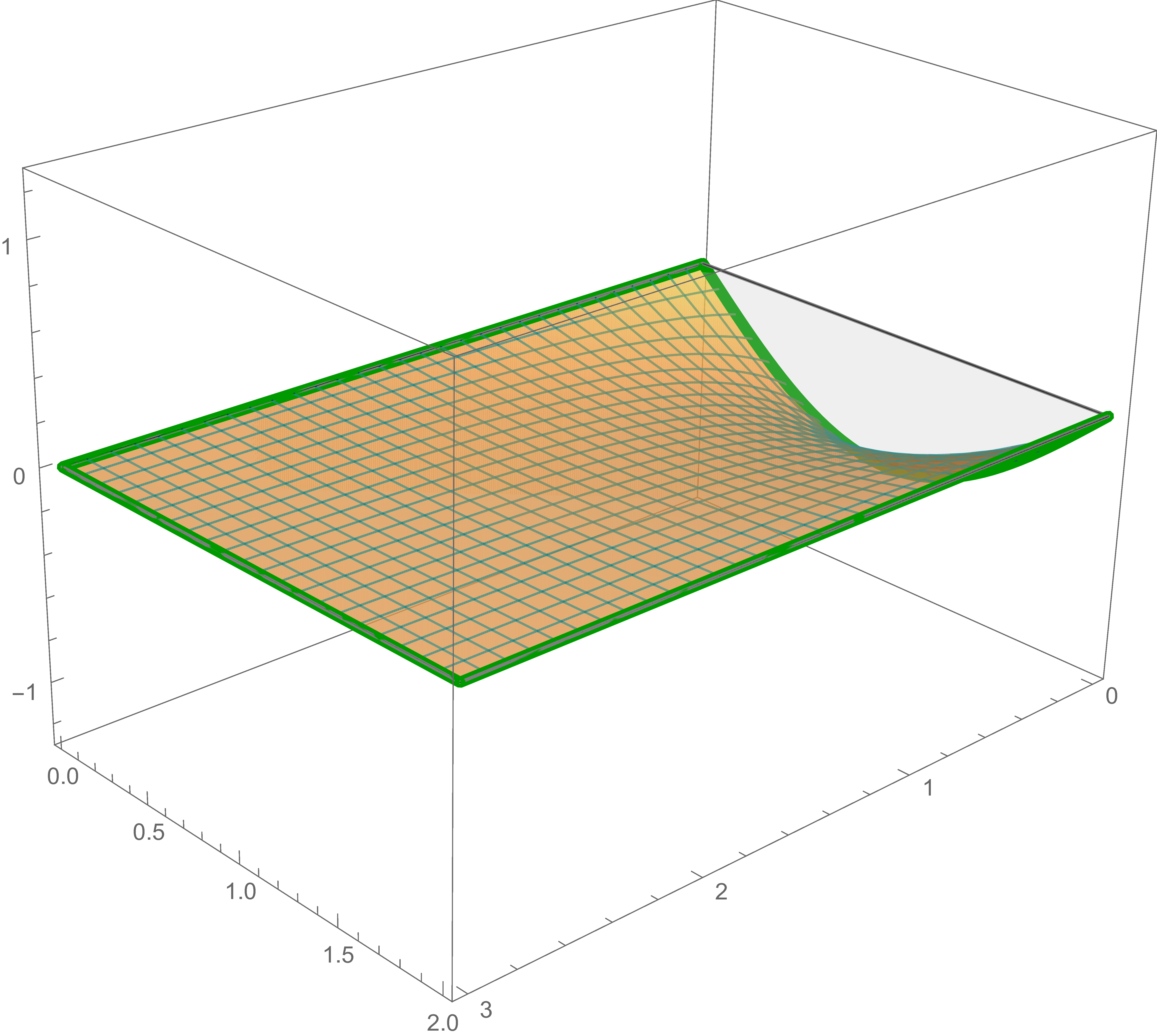

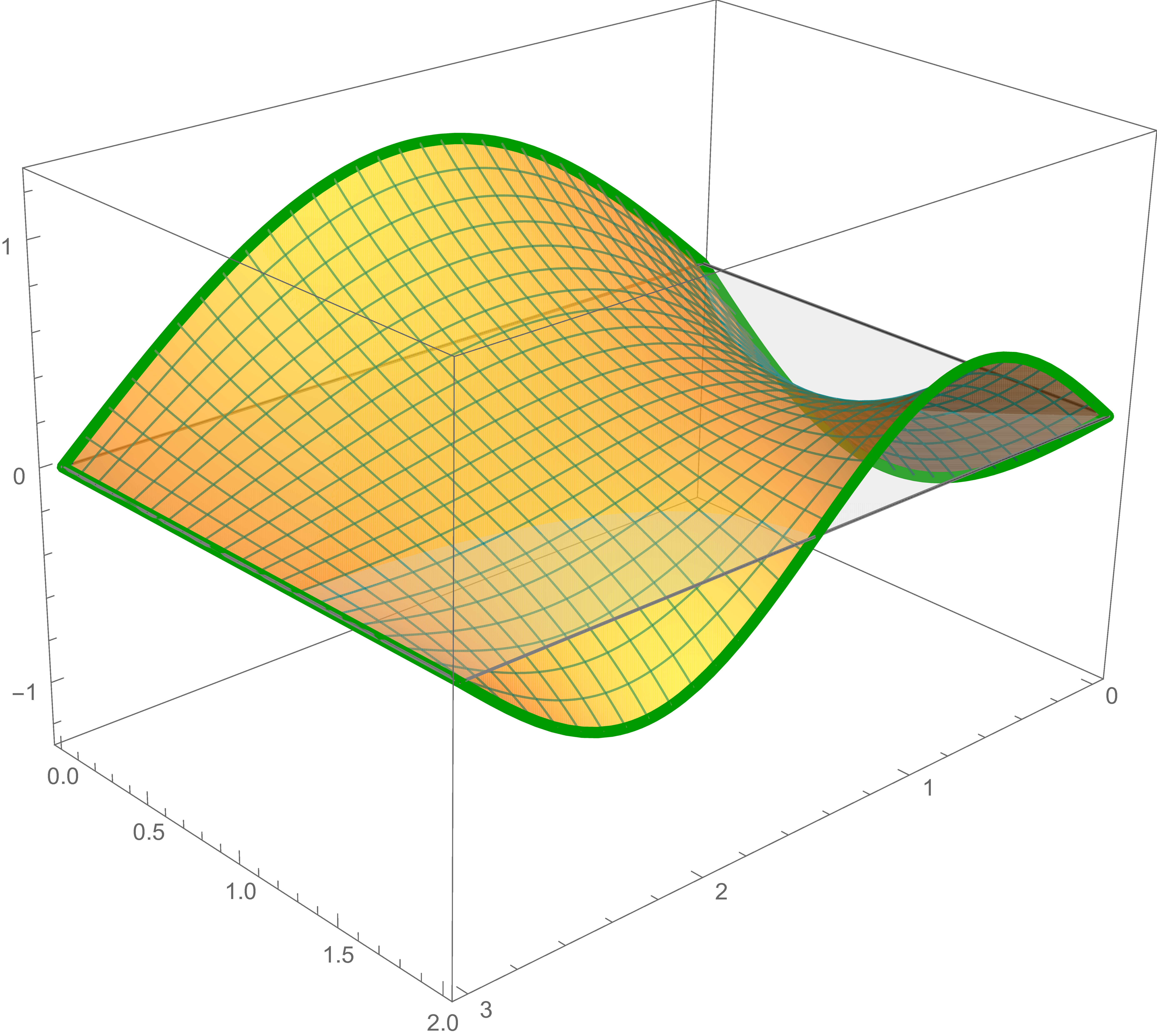
The solution of Laplace's equation that satisfies the fourth boundary condition is \[ -\frac{1}{2} \sin \left( \pi y \right) \frac{\sinh \left(\pi x \right)}{\sinh\left(\pi \, 3 \right)} \]
The fourth solution, the preceding sum and the sum of the first, the second, the third, and the fourth solutions are
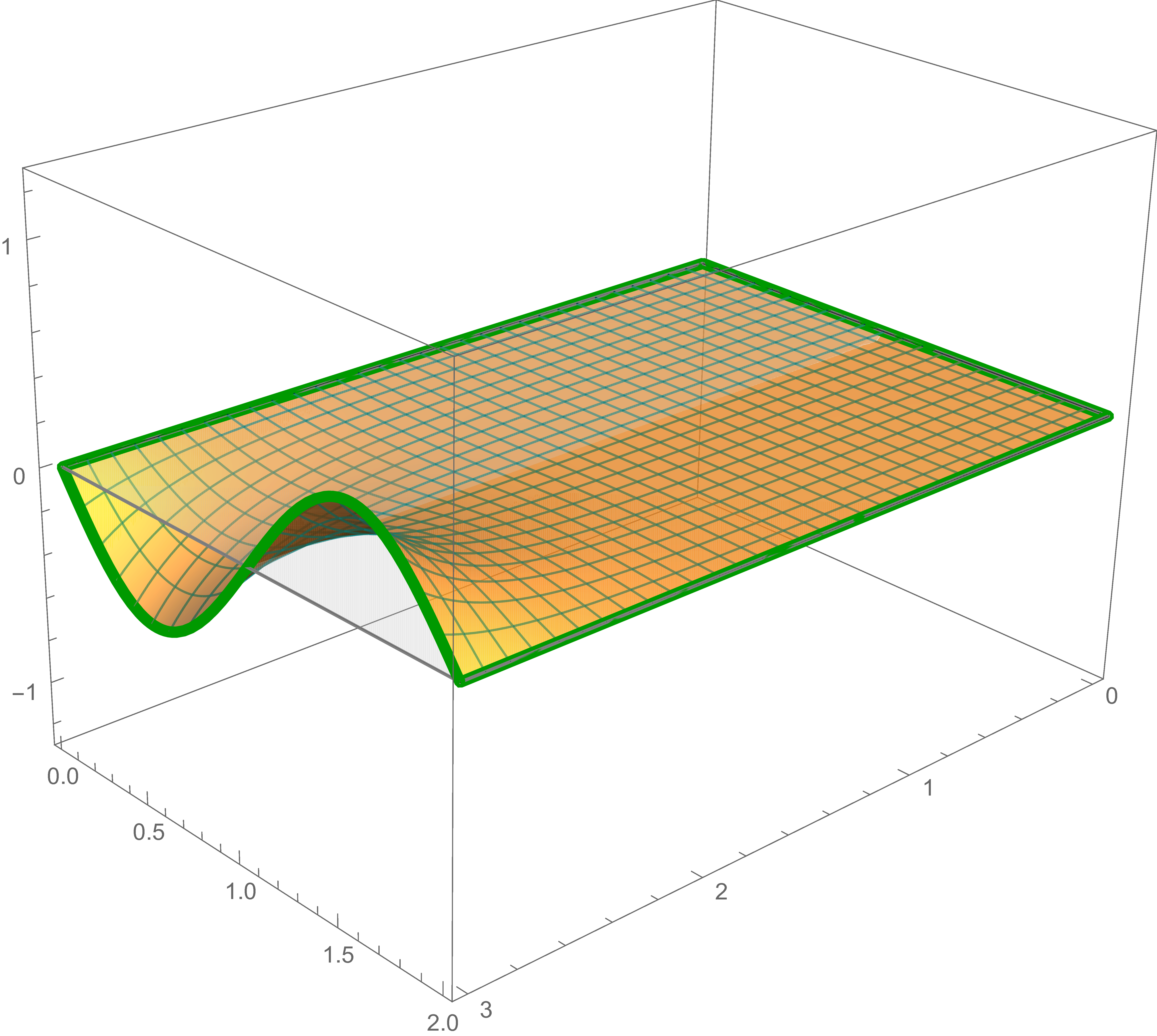

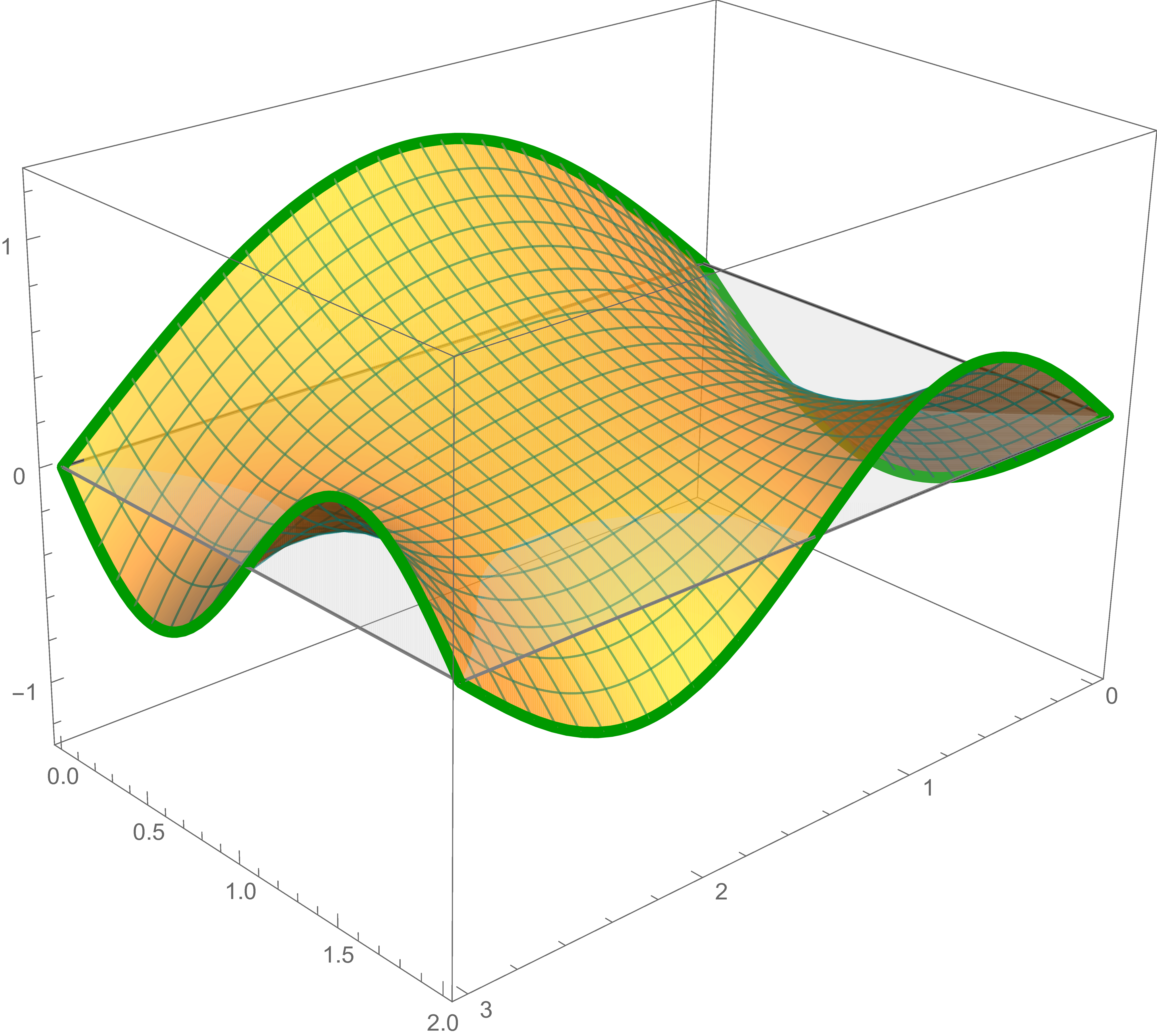
The solution of Laplace's equation that satisfies the "straight edges" boundary condition is \[ \frac{1}{6} \bigl( 3 + 8 x + 9 y - 5 x y \bigr) \]
The solution to the "straight edges" boundary condition, the preceding sum, and the sum of the first, the second, the third, the fourth, and the solution to the "straight edges" boundary conditions are
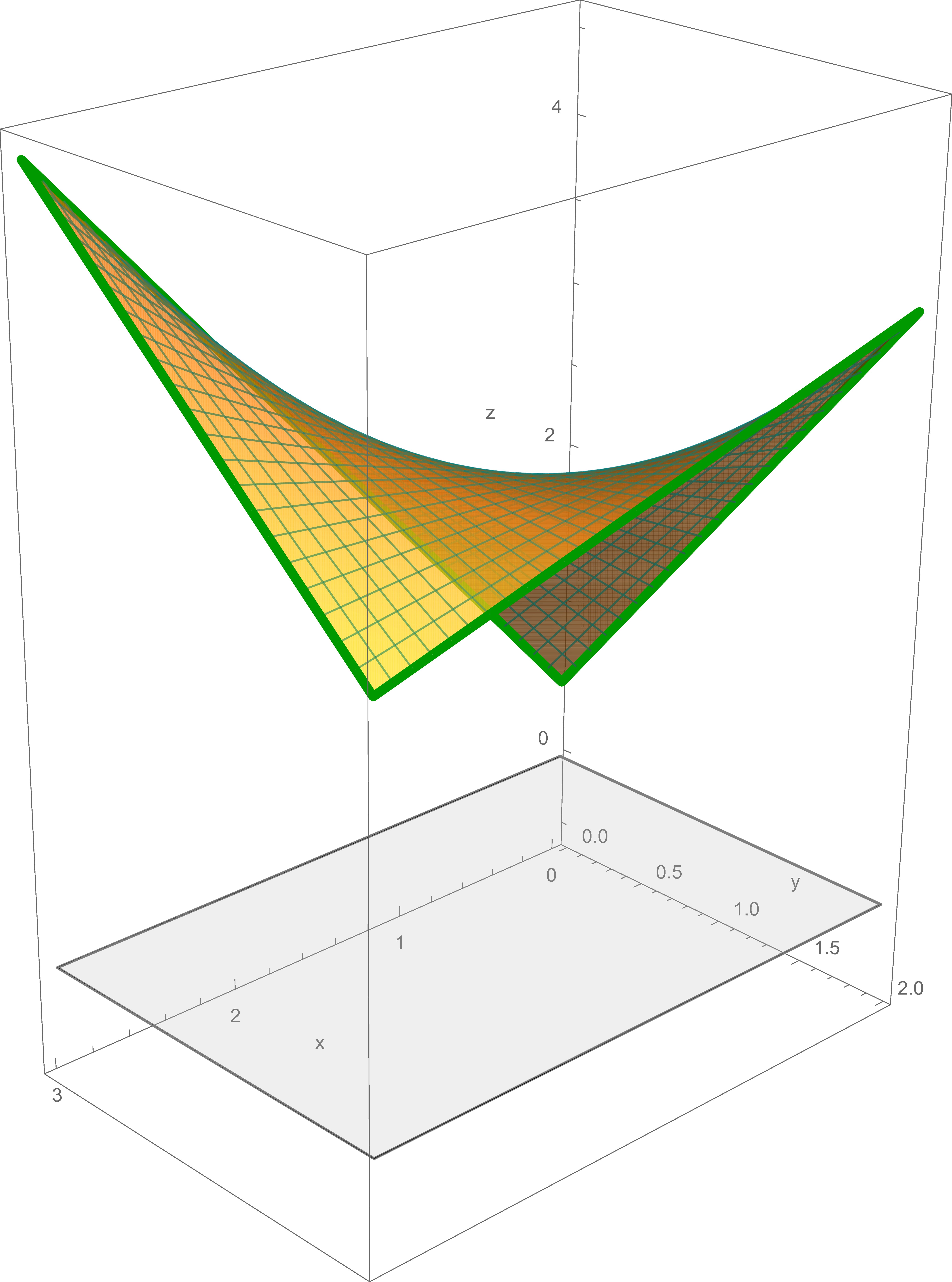
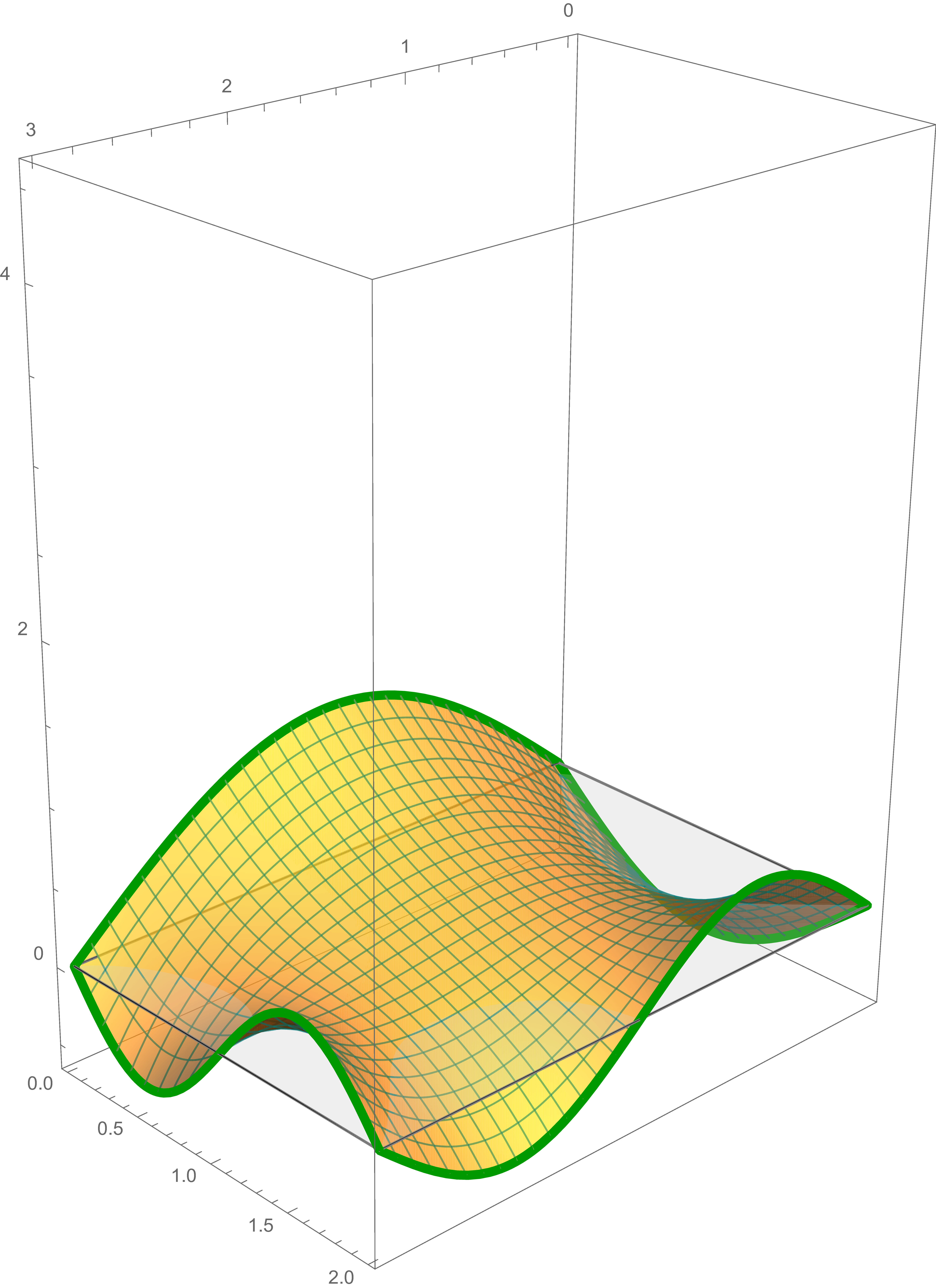

Finally, the solution of the given boundary value problem for Laplace's equation is the sum of the preceding solutions: \begin{align*} \sin \left(\frac{\pi}{3} x\right) & \frac{\sinh \left(\frac{\pi}{3}(2-y)\right)}{\sinh\left(\frac{\pi }{3}\, 2 \right)} +\frac{1}{2} \sin \left( \frac{2\pi}{3} x \right) \frac{\sinh \left(\frac{2\pi}{3}(2-y)\right)}{\sinh\left(\frac{2\pi }{3}\, 2 \right)} \\ &\qquad - \frac{2}{3} \sin \left( \frac{\pi}{2} y \right) \frac{\sinh \left(\frac{\pi}{2}(3-x)\right)}{\sinh\left(\frac{\pi}{2}\, 3 \right)} -\frac{1}{2} \sin \left( \pi y \right) \frac{\sinh \left(\pi x \right)}{\sinh\left(\pi \, 3 \right)} +\frac{1}{6} \bigl( 3 + 8 x + 9 y - 5 x y \bigr) \end{align*} We close this section with a big graph of this solution:
