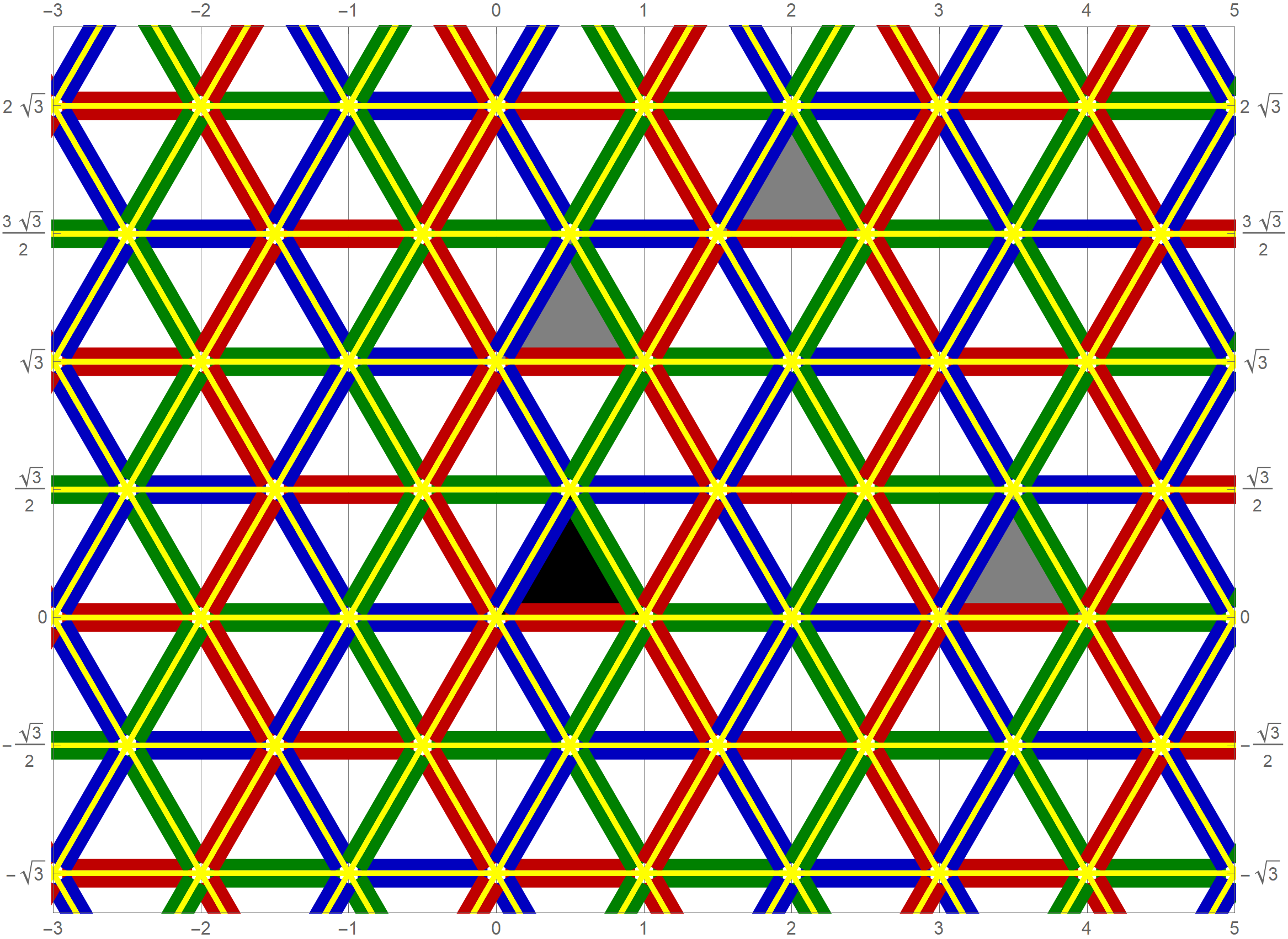
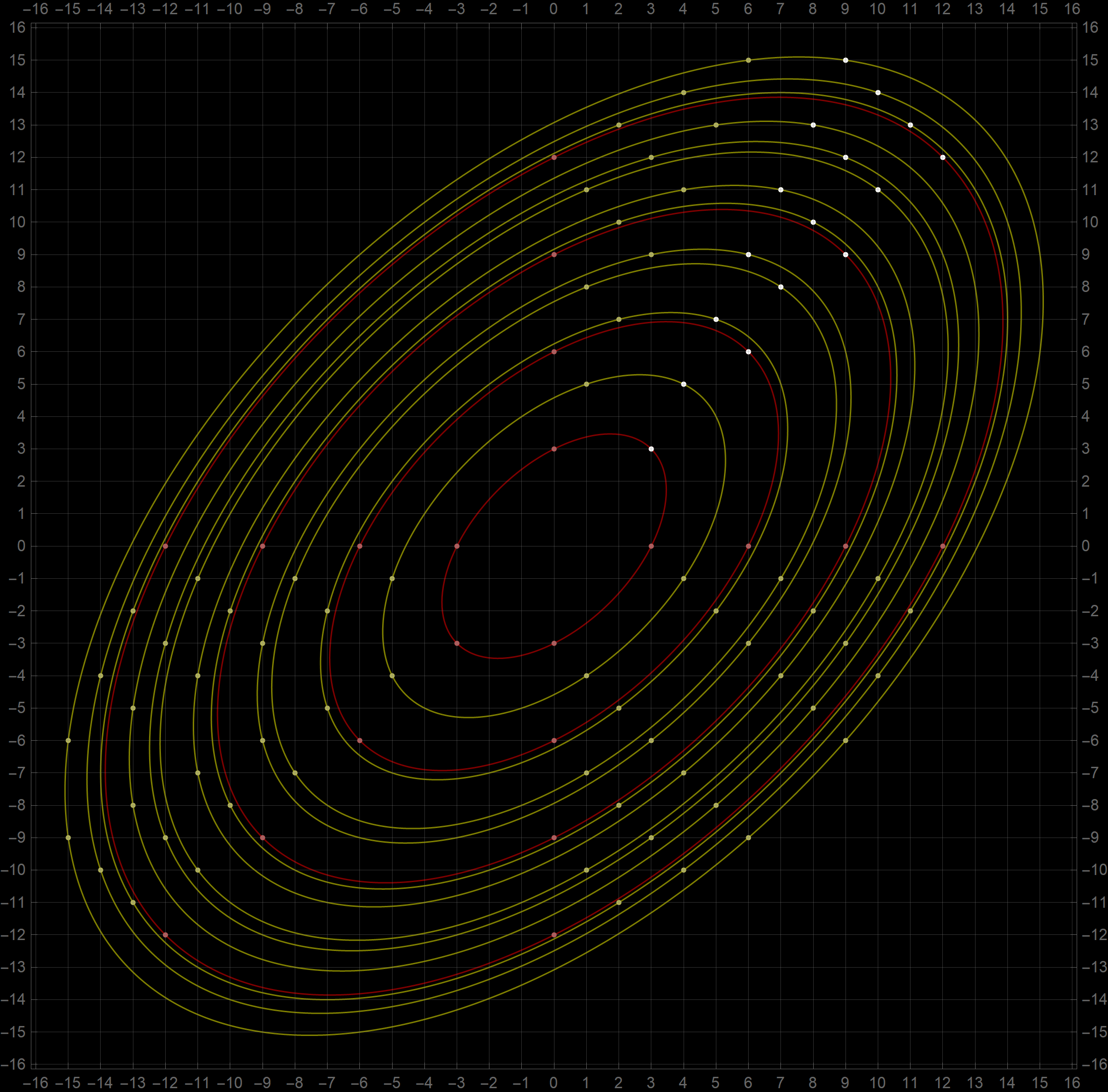
The first eigenvalue is simple. The $(m,n)$ pairs that we used to construct the eigenfunction are \[ (3, 3), \quad (3, 0), \quad (-3, 0), \quad (-3, -3), \quad (0, -3), \quad (0, 3). \] The eigenfunction is
\[ \operatorname{im}(x,y) = 2 \sin \left(\frac{2}{3} \pi \left(3 x- \sqrt{3} y\right)\right) - 2 \sin \left(\frac{2}{3} \pi \left(3 x+\sqrt{3} y\right)\right) +2 \sin \left(\frac{4 \pi y}{\sqrt{3}}\right) \]
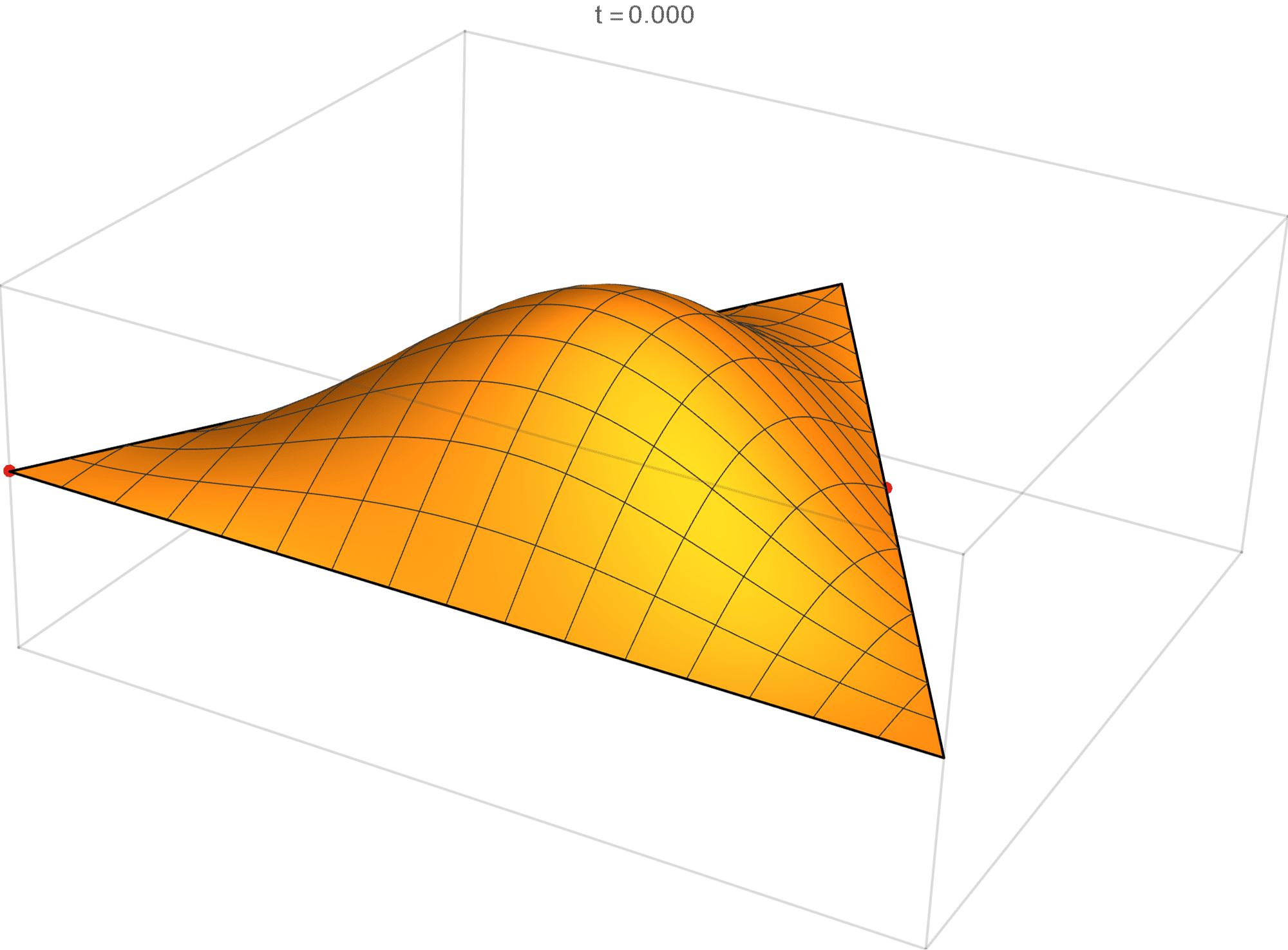
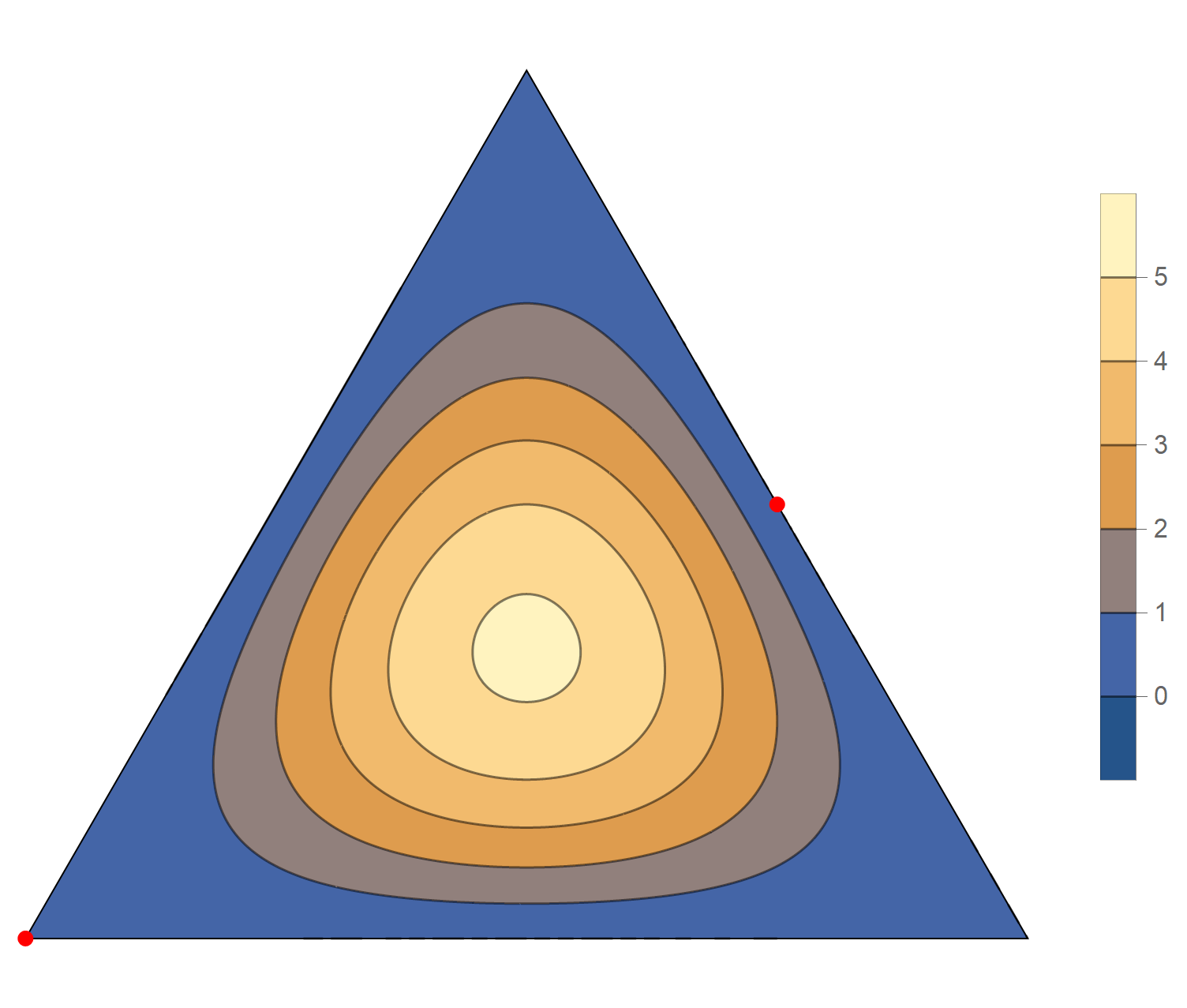
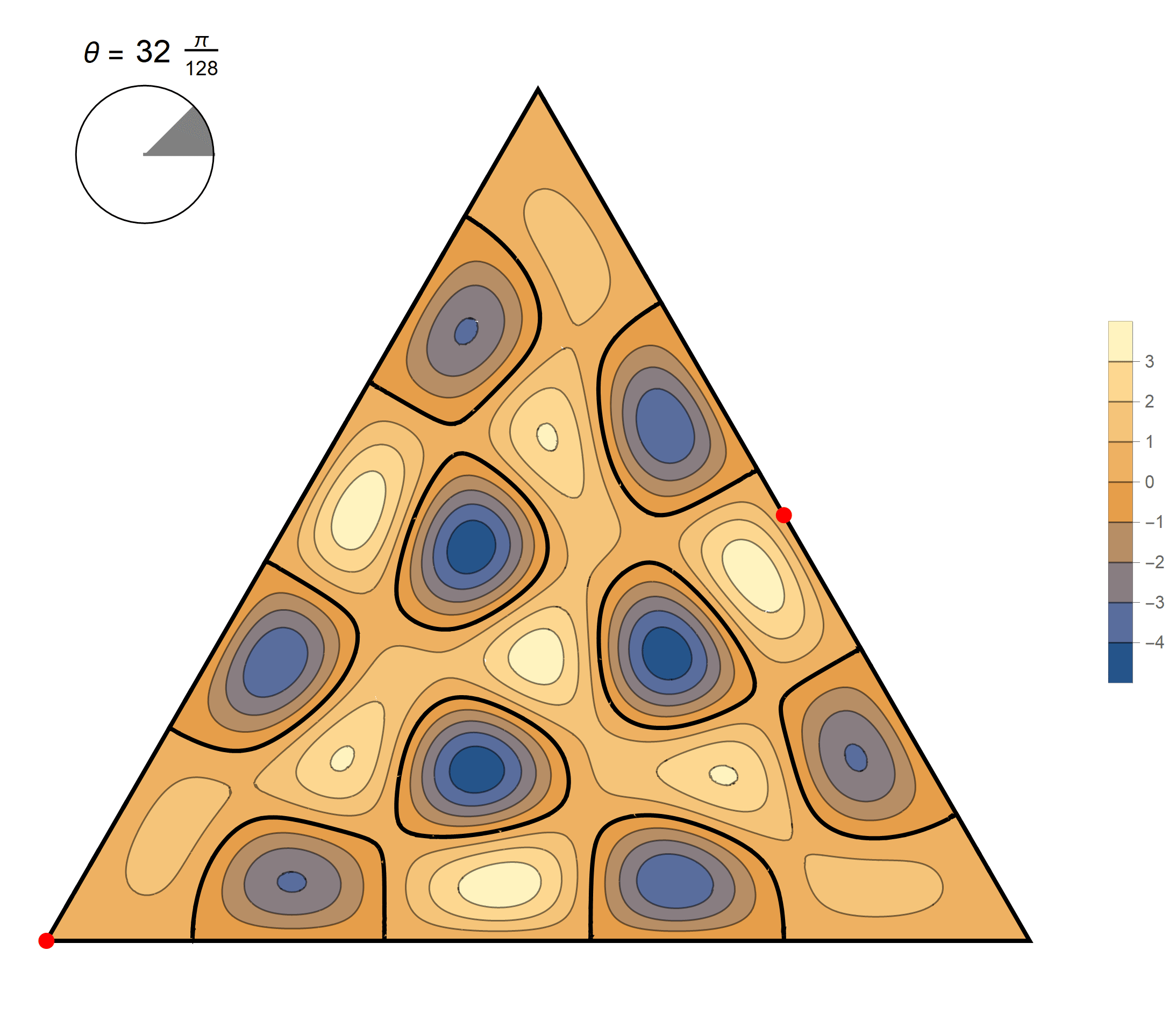
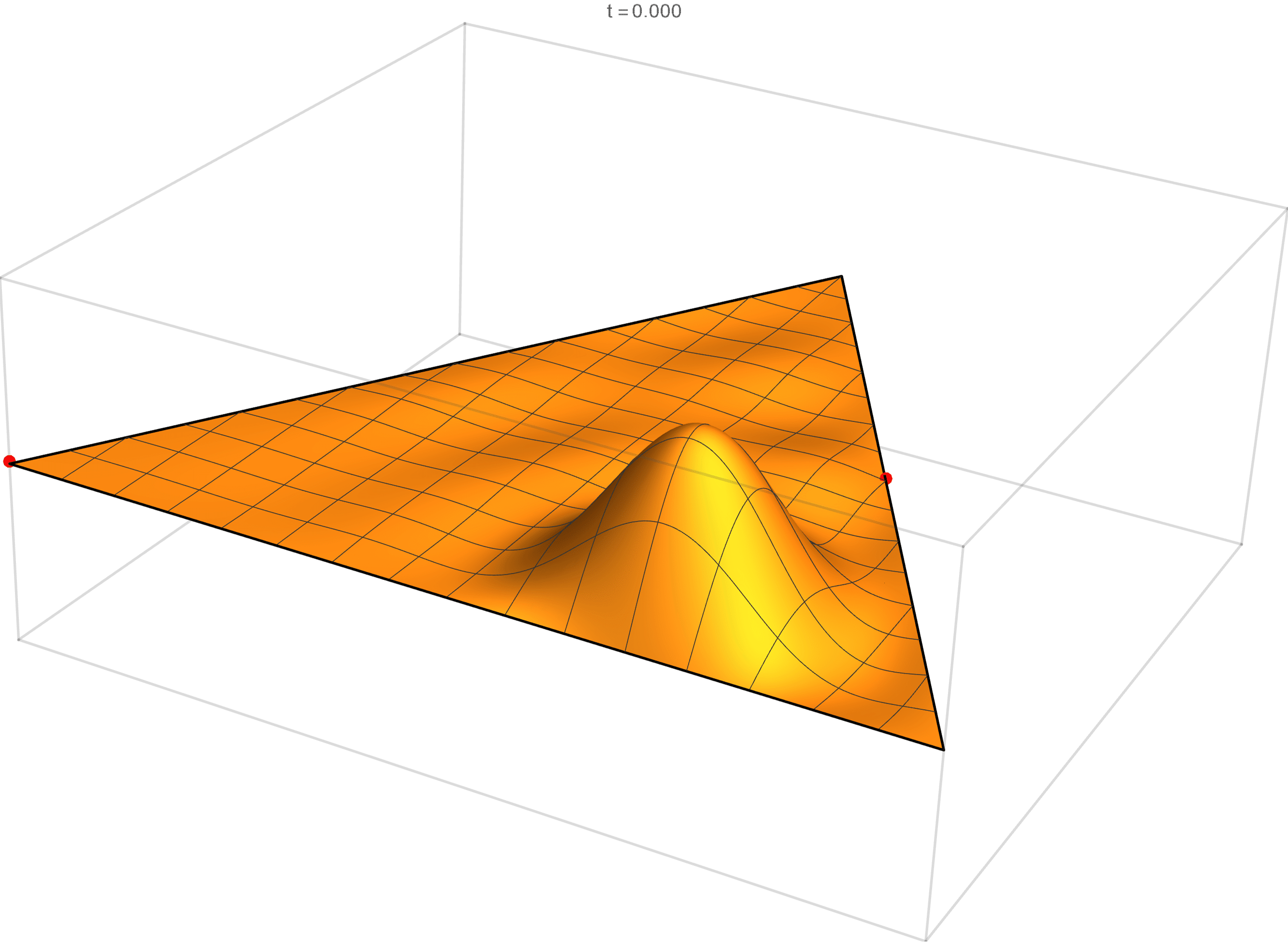
The second eigenvalue has multiplicity 2. The $(m,n)$ pairs that we used to construct the eigenfunction are \[ (4, 5), \quad (4, -1), \quad (-5, -1), \quad (-5, -4), \quad (1, -4), \quad (1, 5). \] The eigenfunctions are
\begin{align*} \operatorname{im}(x,y) & = \sin \left(\frac{2}{3} \pi \left(4 x - 2 \sqrt{3} y\right)\right) -\sin \left(\frac{2}{3} \pi \left(x-3\sqrt{3} y\right)\right) +\sin \left(\frac{2}{3} \pi \left(-5 x-\sqrt{3} y\right)\right) \\ & \qquad \qquad - \sin \left(\frac{2}{3} \pi \left(4 x + 2 \sqrt{3} y\right)\right) -\sin \left(\frac{2}{3} \pi \left(\sqrt{3} y- 5 x\right)\right) +\sin \left(\frac{2}{3} \pi \left(x+3 \sqrt{3} y\right)\right) \\ \operatorname{re}(x,y) & = \cos \left(\frac{2}{3} \pi \left(4 x - 2 \sqrt{3} y\right)\right) -\cos \left(\frac{2}{3} \pi \left(x-3\sqrt{3} y\right)\right) +\cos \left(\frac{2}{3} \pi \left(-5 x-\sqrt{3} y\right)\right) \\ & \qquad \qquad -\cos \left(\frac{2}{3} \pi \left(4 x+2 \sqrt{3} y\right)\right) -\cos \left(\frac{2}{3} \pi \left( \sqrt{3} y - 5 x\right)\right)+\cos \left(\frac{2}{3} \pi \left(x+3 \sqrt{3} y\right)\right) \end{align*}
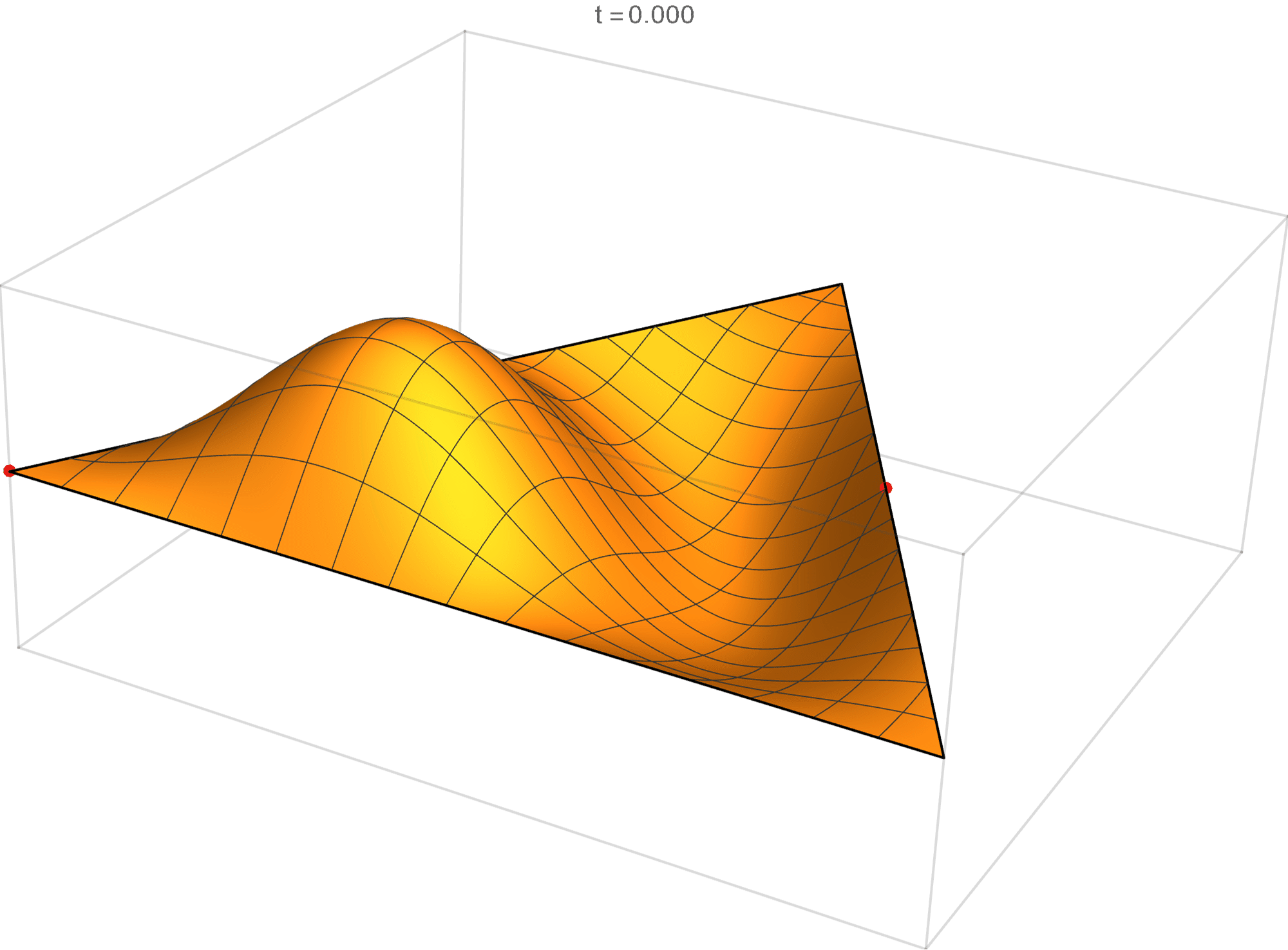
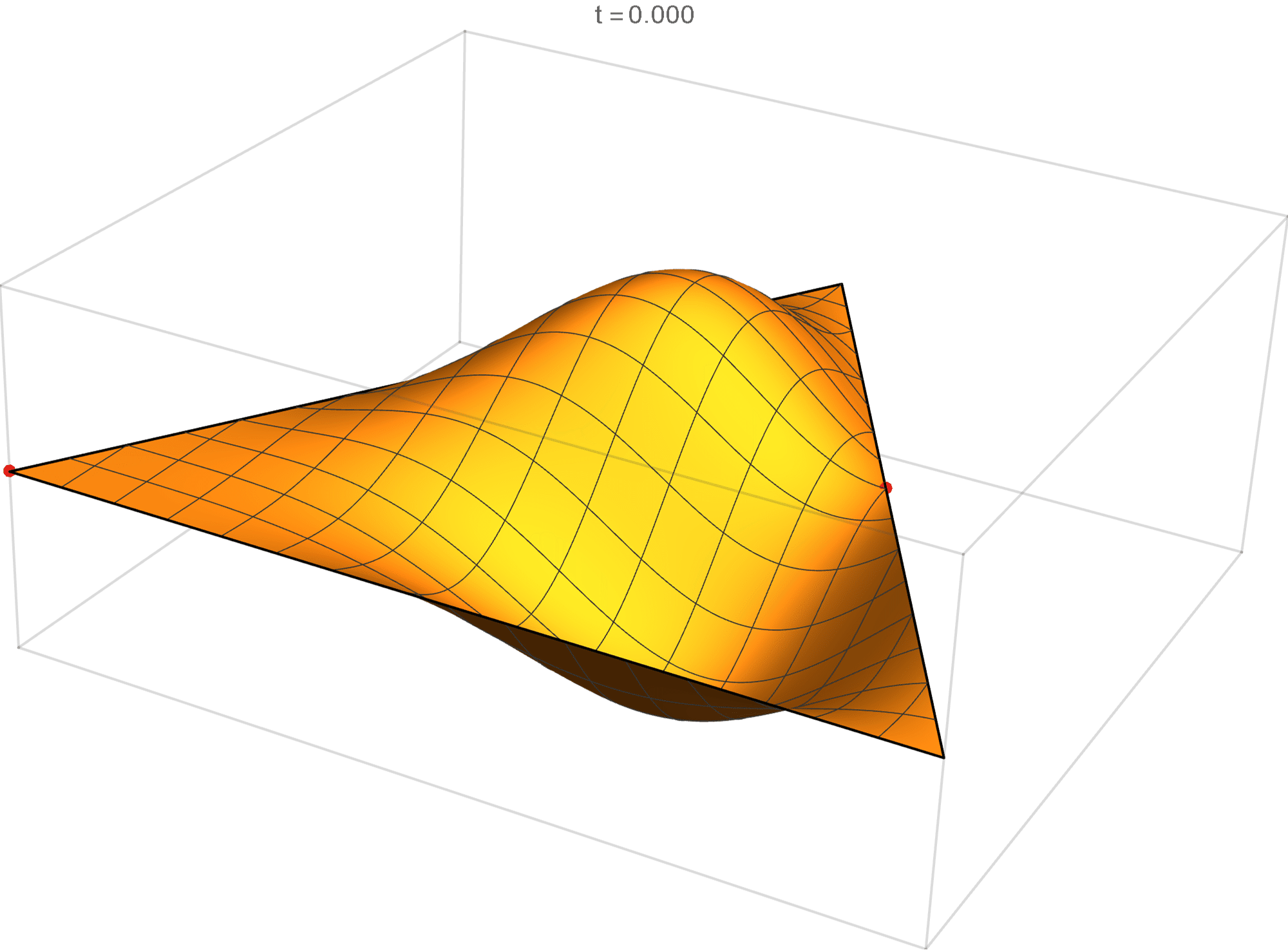
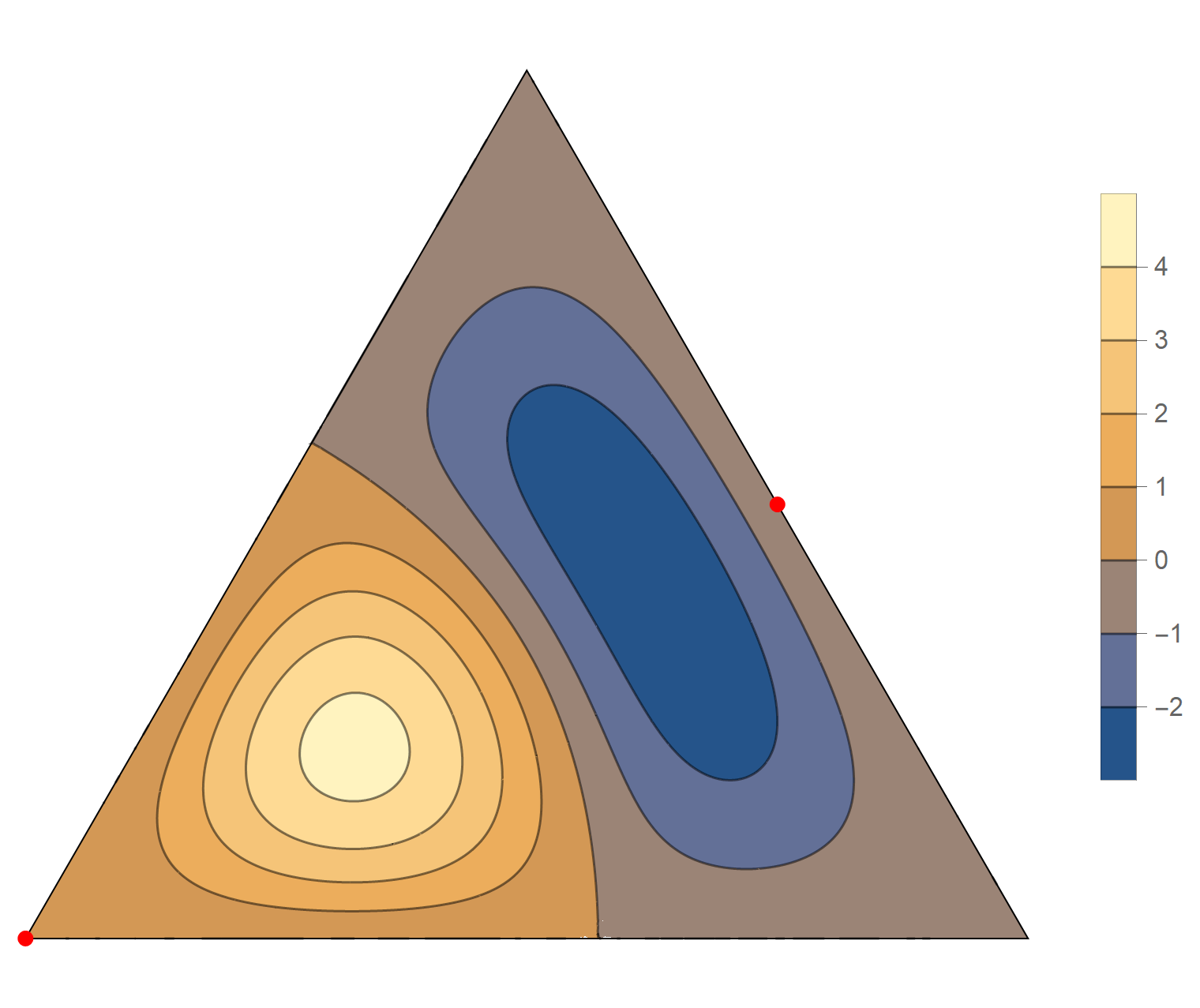
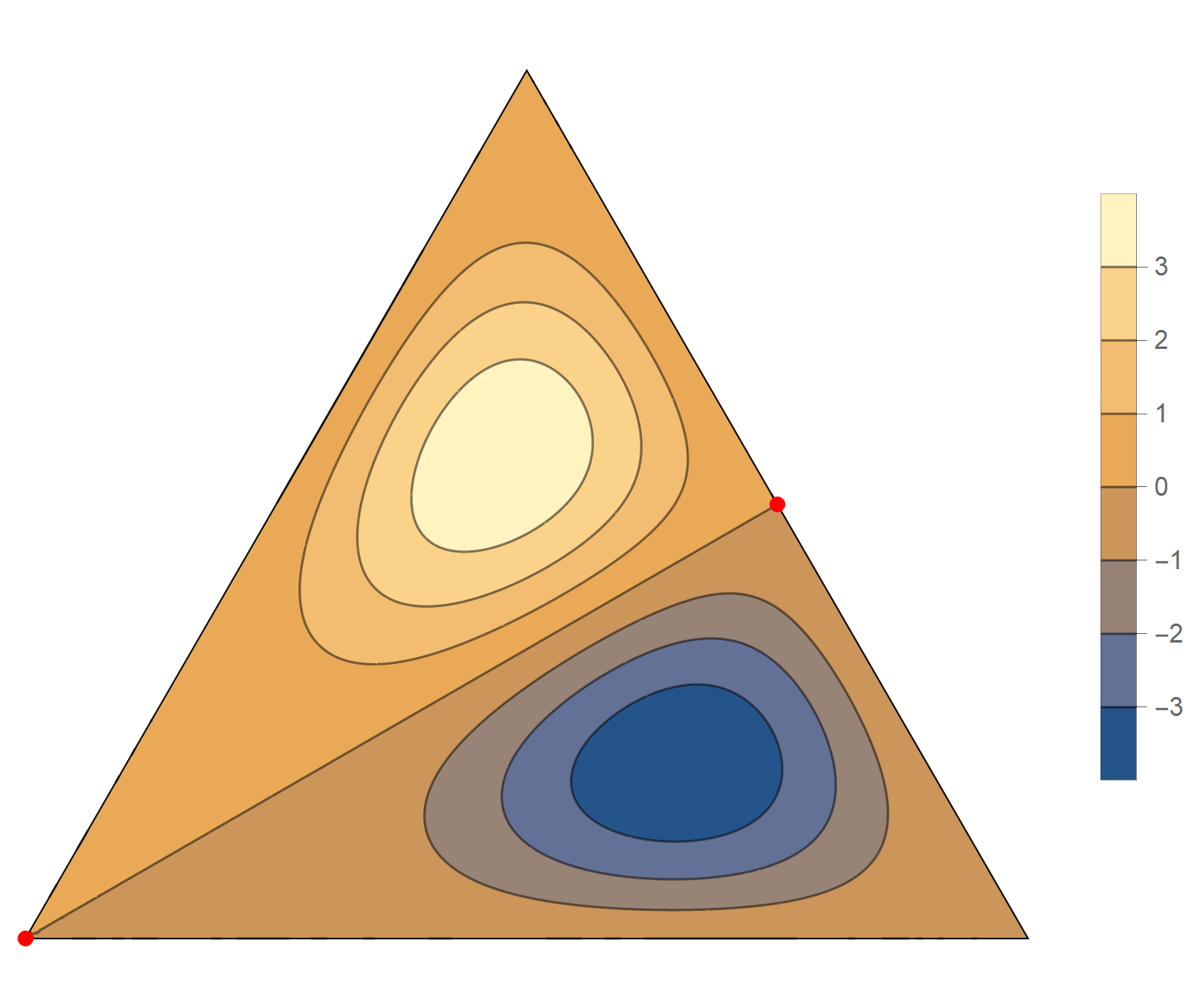
We review the entire two dimensional eigenspace as follows:
\[(\cos\theta)\operatorname{im}(x,y) +(\sin\theta) \operatorname{re}(x,y) \quad \text{as a function of} \quad \theta \in [0,2\pi).\]
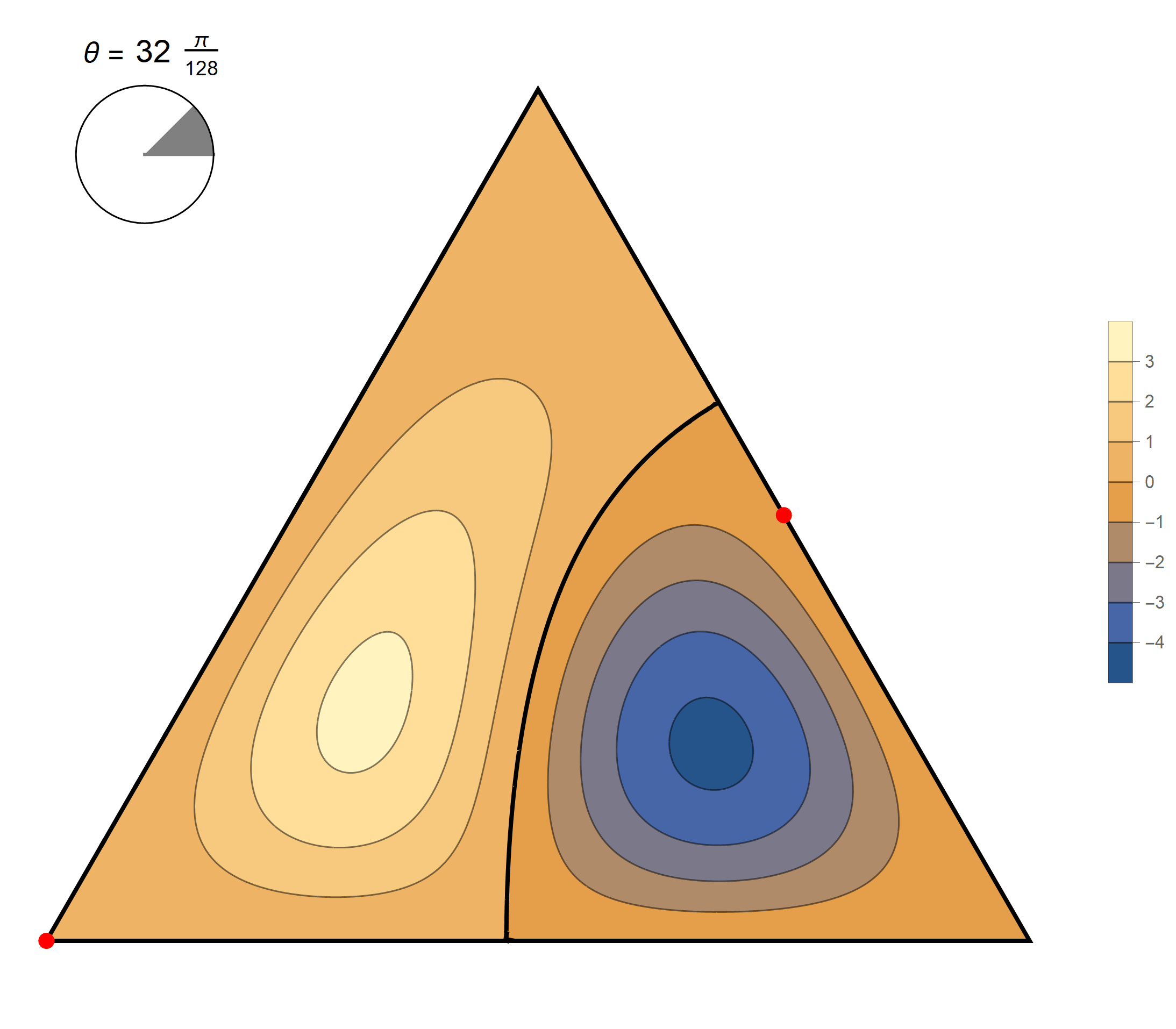
The third eigenvalue is simple. The $(m,n)$ pairs that we used to construct the eigenfunction are \[ (6, 6), \quad (6, 0), \quad (-6, 0), \quad (-6, -6), \quad (0,-6), \quad (0,6). \] The eigenfunctions are
\[ \operatorname{im}(x,y) = 2 \sin \left(\frac{2}{3} \pi \left(6 x-2 \sqrt{3} y\right)\right)-2 \sin \left(\frac{2}{3} \pi \left(6 x+2 \sqrt{3} y\right)\right)+2 \sin \left(\frac{8 \pi y}{\sqrt{3}}\right) \]
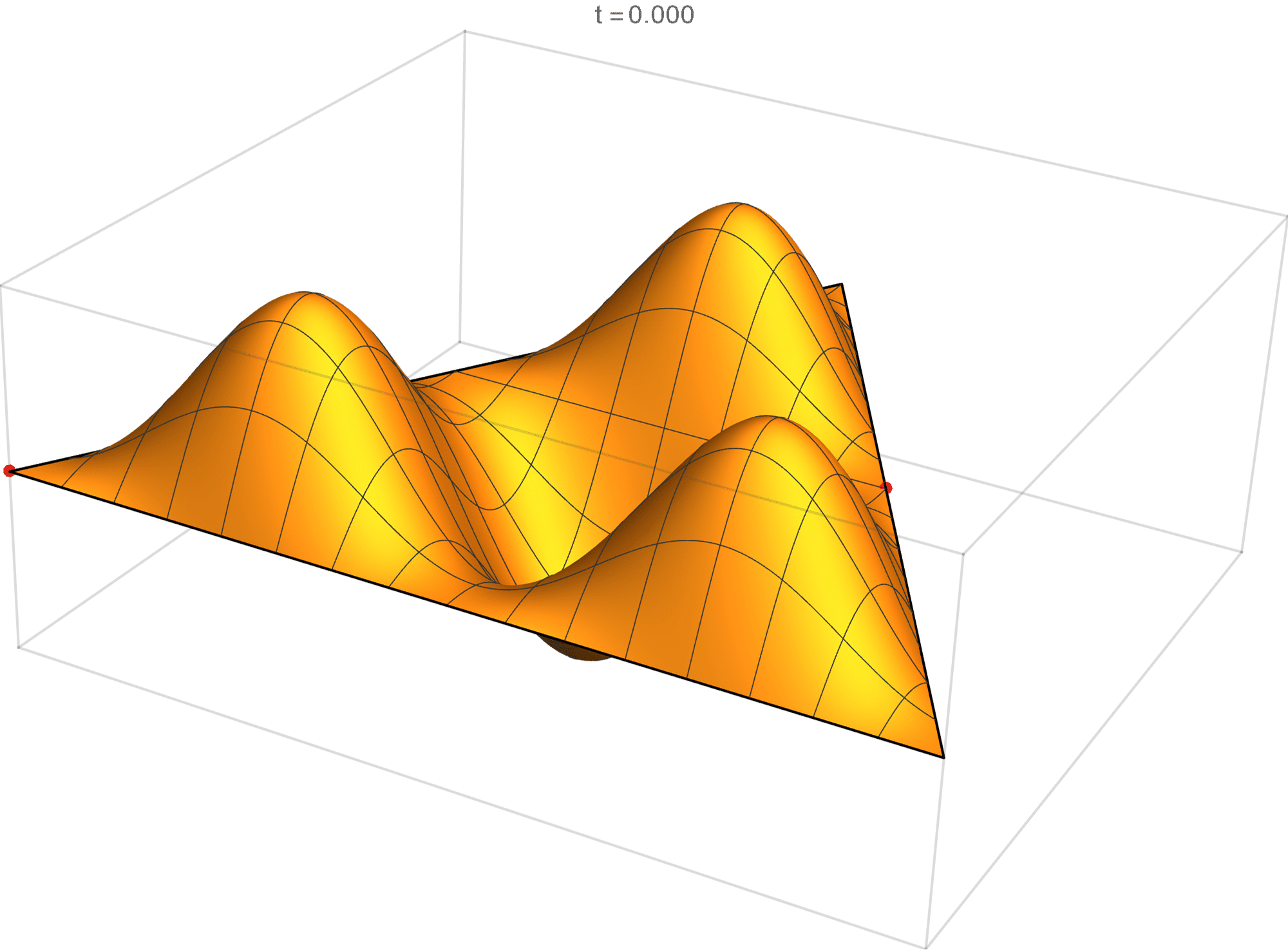
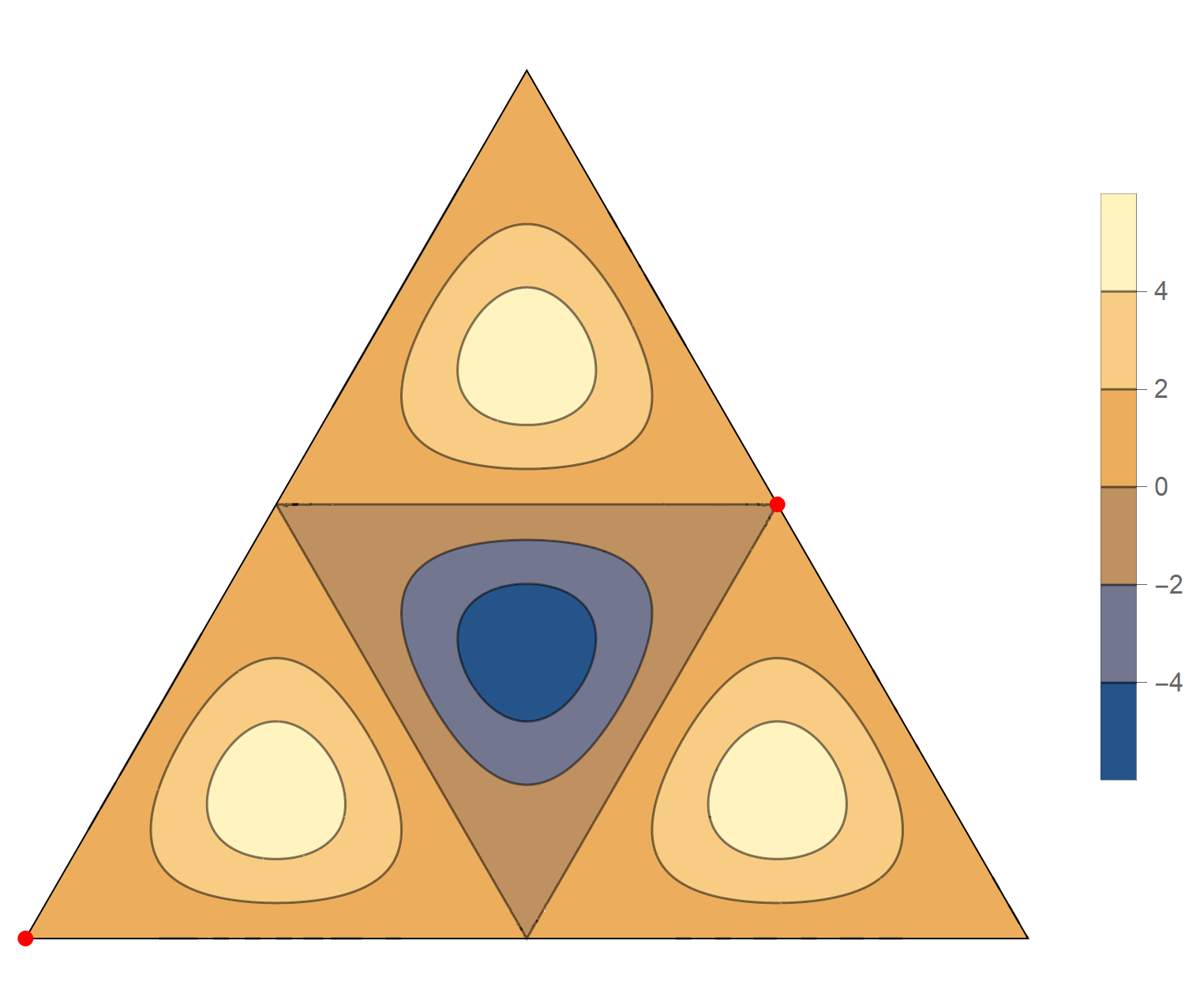
The fourth eigenvalue has multiplicity 2. The $(m,n)$ pairs that we used to construct the eigenfunction are \[ (5, 7), \quad (5, -2), \quad (-7, -2), \quad (-7, -5), \quad (2, -5), \quad (2, 7). \] The eigenfunctions are
\begin{align*} \operatorname{im}(x,y) & = -\sin \left(\frac{2}{3} \pi \left(2 x - 4 \sqrt{3} y\right)\right) +\sin \left(\frac{2}{3} \pi \left(5 x-3 \sqrt{3} y\right)\right) +\sin \left(\frac{2}{3} \pi \left(-7 x-\sqrt{3} y\right)\right)\\ & \qquad\qquad -\sin\left(\frac{2}{3} \pi \left(\sqrt{3} y-7 x\right)\right) -\sin \left(\frac{2}{3} \pi \left(5 x+3 \sqrt{3} y\right)\right) +\sin \left(\frac{2}{3} \pi \left(2 x+4 \sqrt{3} y\right)\right) \\ \operatorname{re}(x,y) & = -\cos \left(\frac{2}{3} \pi \left(2 x-4 \sqrt{3} y\right)\right) +\cos \left(\frac{2}{3} \pi \left(5 x-3 \sqrt{3} y\right)\right) +\cos \left(\frac{2}{3} \pi \left(-7 x-\sqrt{3} y\right)\right)\\ & \qquad\qquad -\cos \left(\frac{2}{3} \pi \left(\sqrt{3} y-7 x\right)\right) -\cos \left(\frac{2}{3} \pi \left(5 x+3 \sqrt{3} y\right)\right) +\cos \left(\frac{2}{3} \pi \left(2 x+4 \sqrt{3} y\right)\right) \end{align*}
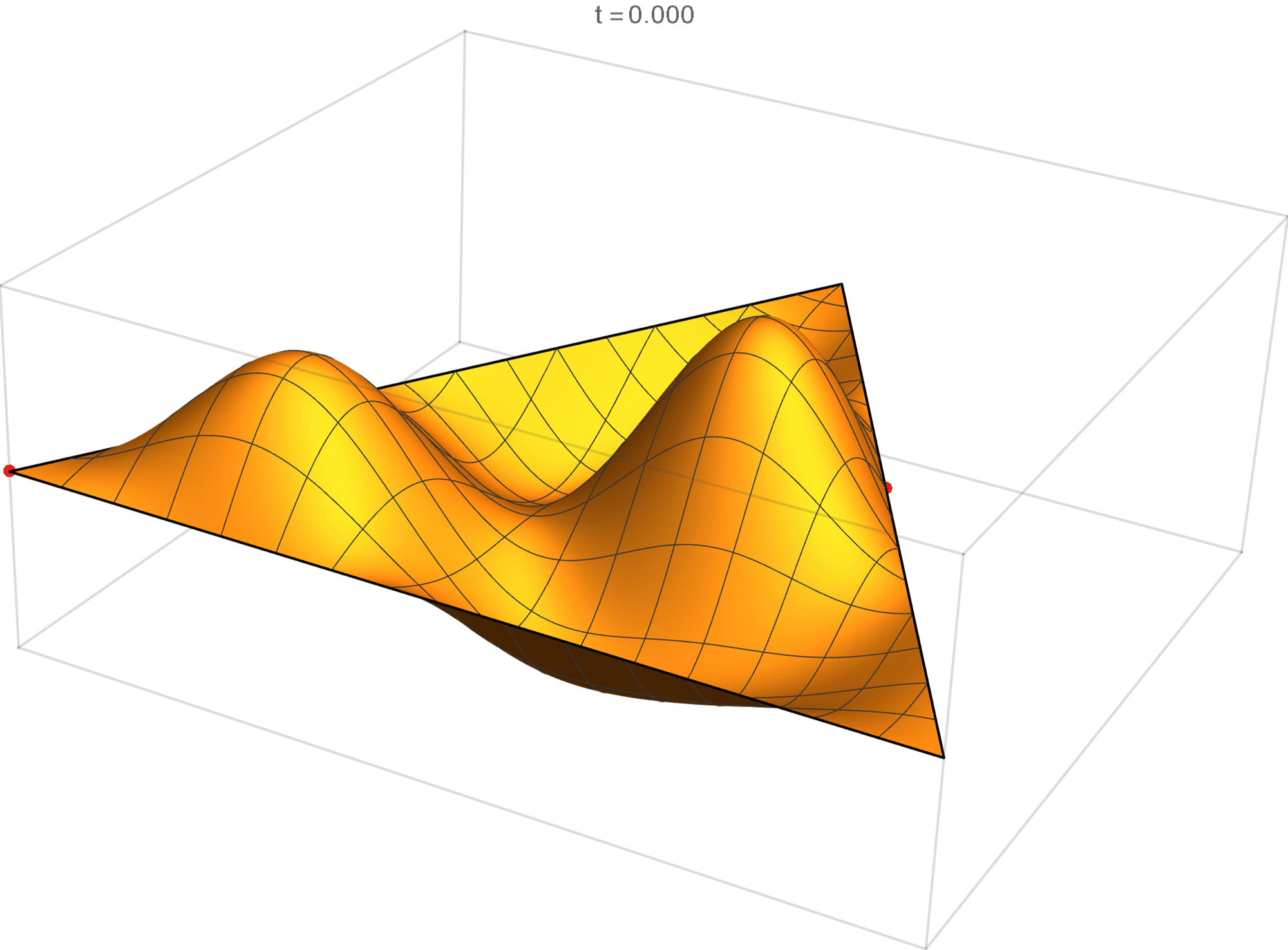
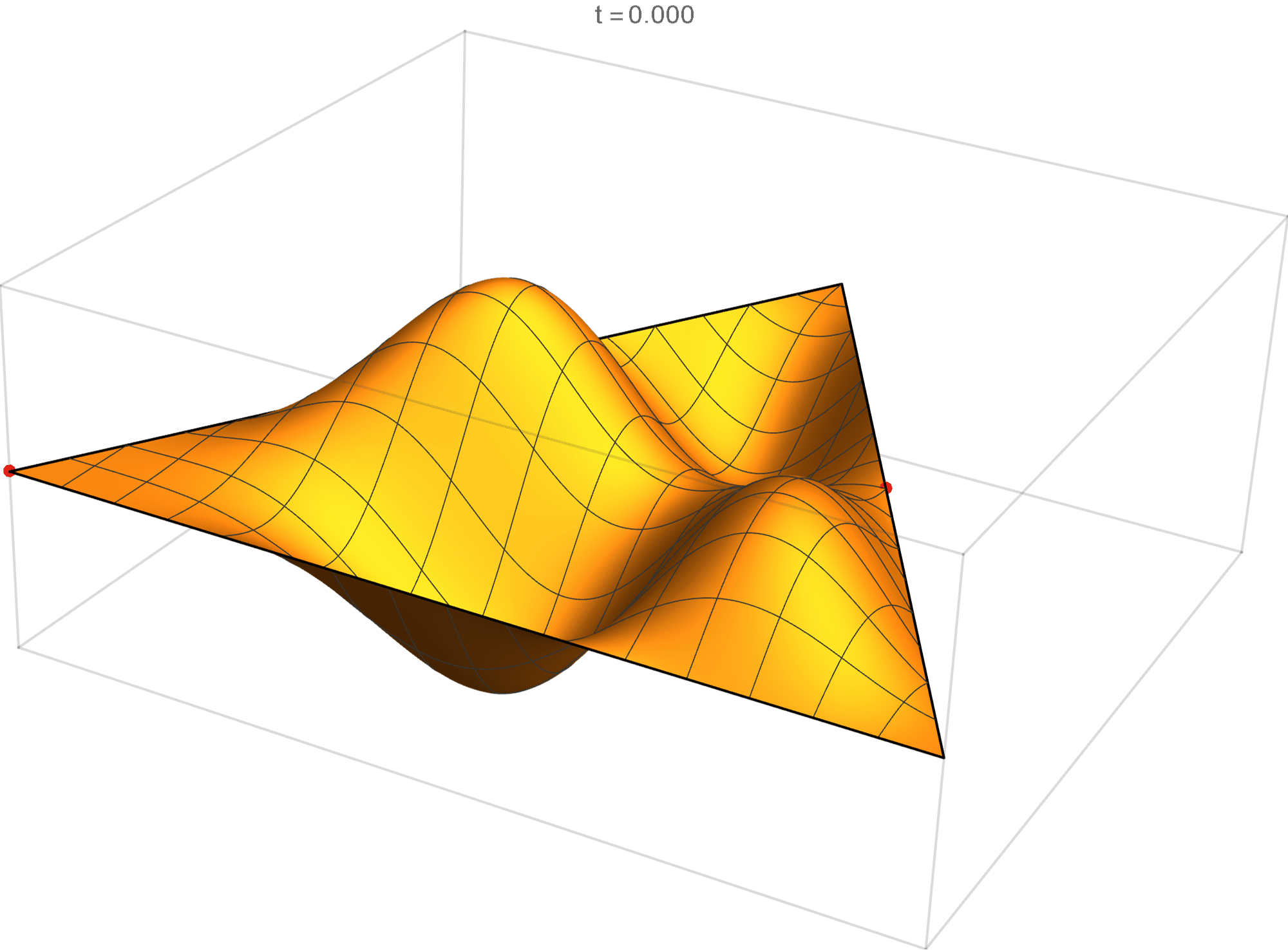
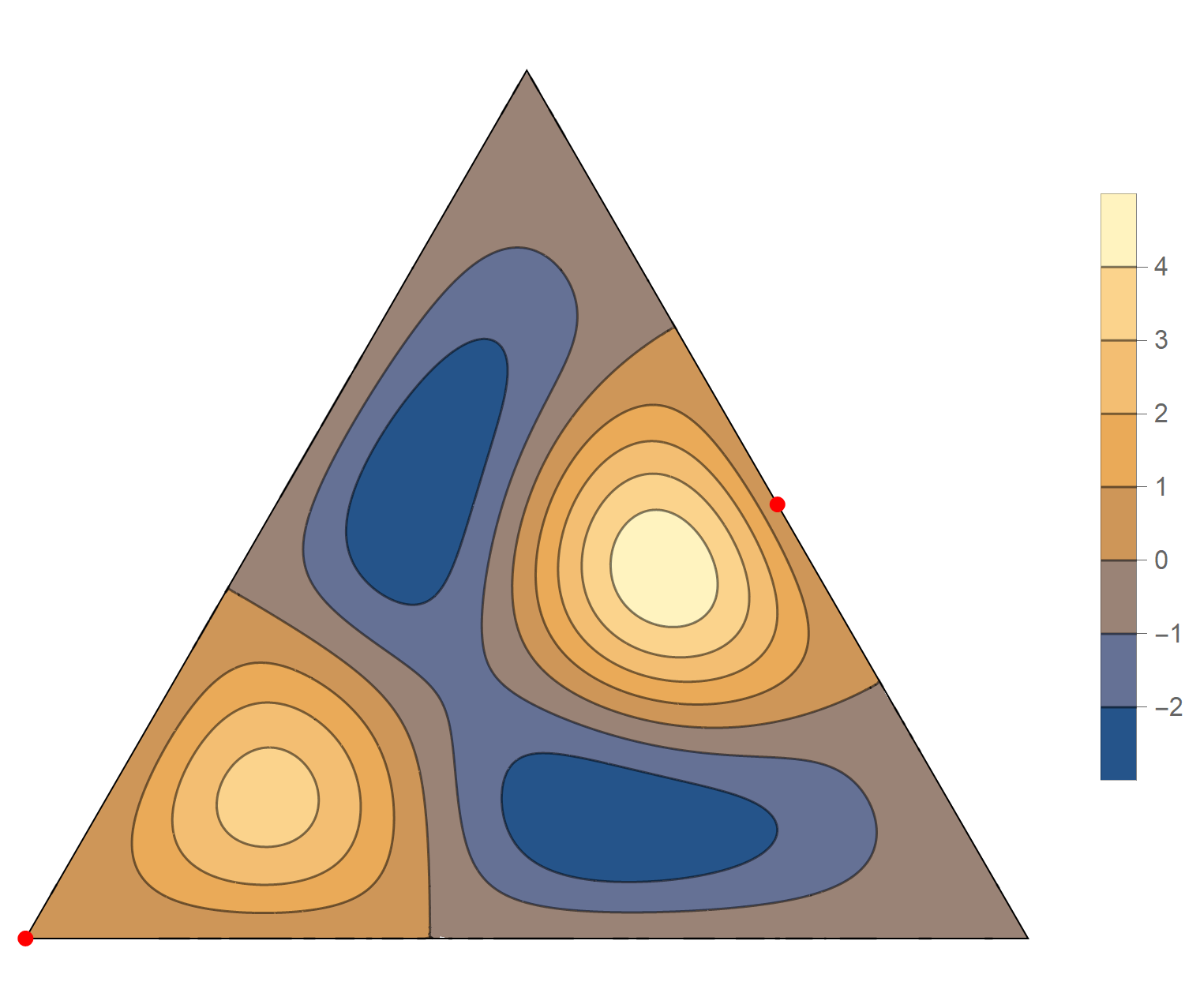
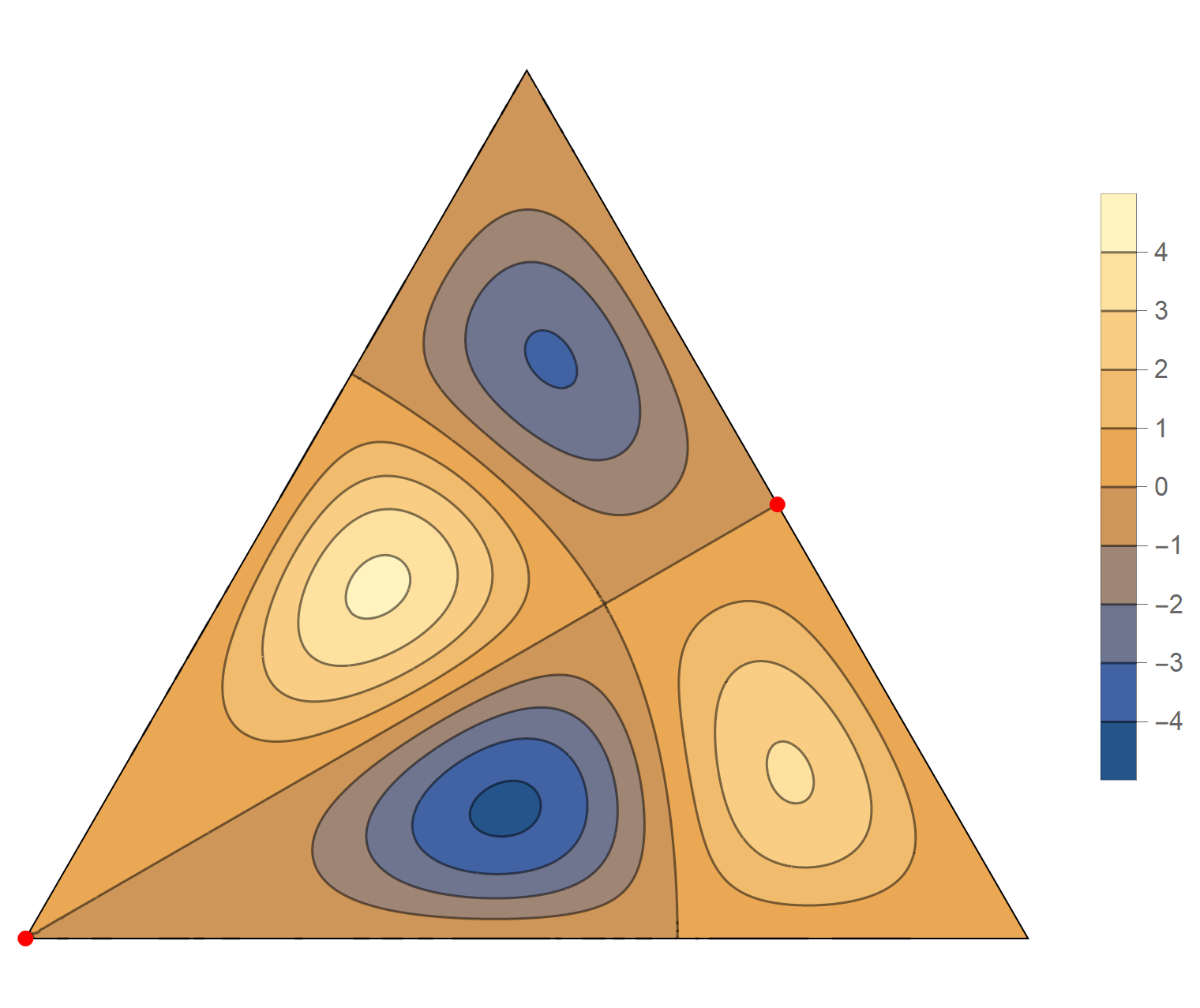
We review the entire two dimensional eigenspace as follows:
\[(\cos\theta)\operatorname{im}(x,y) +(\sin\theta) \operatorname{re}(x,y) \quad \text{as a function of} \quad \theta \in [0,2\pi).\]
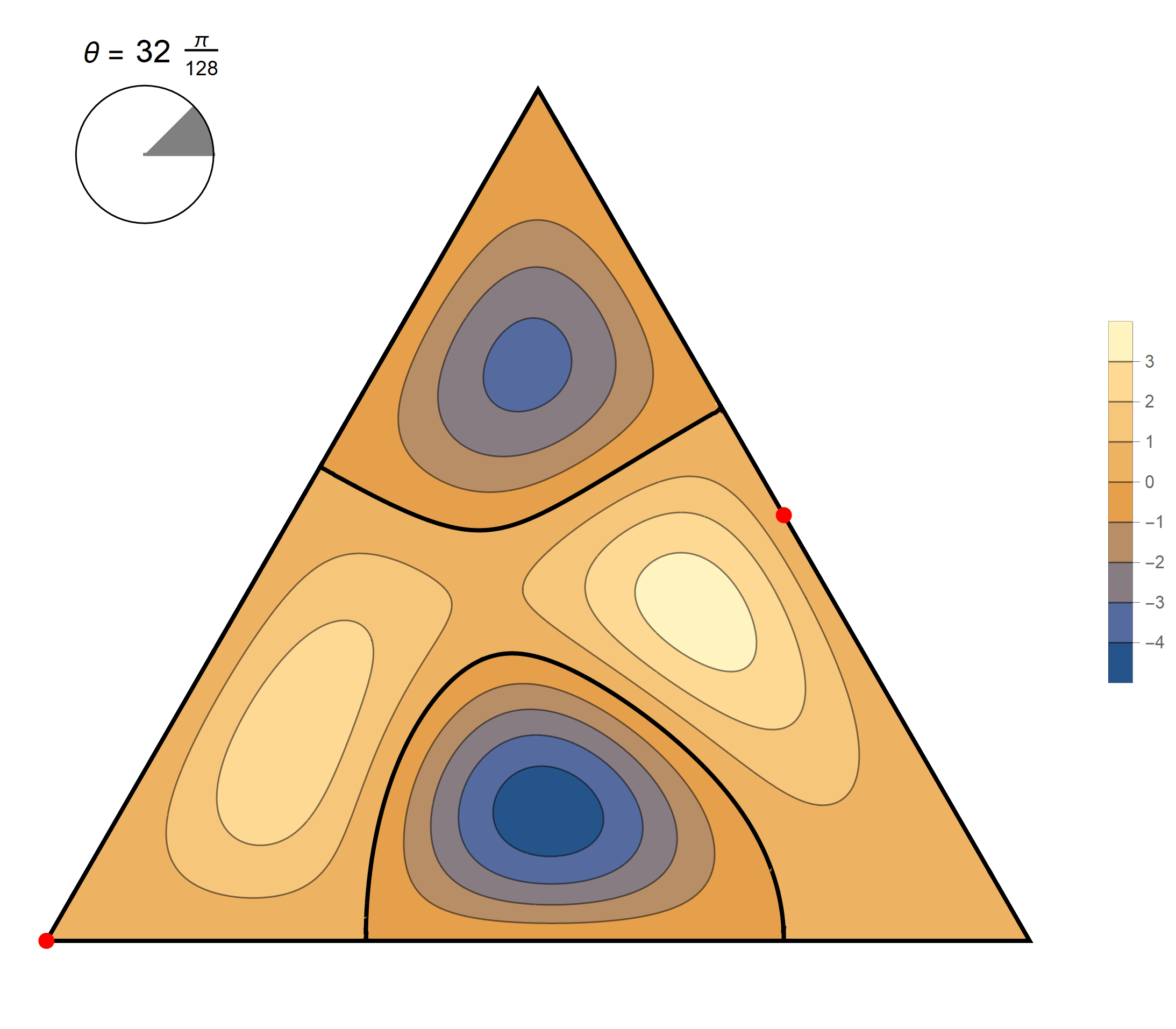
The fifth eigenvalue has multiplicity 2. The $(m,n)$ pairs that we used to construct the eigenfunction are \[ (7, 8), \quad (7, -1), \quad (-8, -1), \quad (-8, -7), \quad (1, -7), \quad (1, 8). \] The eigenfunctions are
\begin{align*} \operatorname{im}(x,y) & = -\sin \left(\frac{2}{3} \pi \left(x-5 \sqrt{3} y\right)\right) +\sin \left(\frac{2}{3} \pi \left(7 x-3 \sqrt{3} y\right)\right) +\sin \left(\frac{2}{3} \pi \left(-8 x-2 \sqrt{3} y\right)\right) \\ & \qquad\qquad -\sin\left(\frac{2}{3} \pi \left(2 \sqrt{3} y-8 x\right)\right) -\sin \left(\frac{2}{3} \pi \left(7 x+3 \sqrt{3} y\right)\right) +\sin \left(\frac{2}{3} \pi \left(x+5 \sqrt{3} y\right)\right) \\ \operatorname{re}(x,y) & = -\cos \left(\frac{2}{3} \pi \left(x-5 \sqrt{3} y\right)\right) +\cos \left(\frac{2}{3} \pi \left(7 x-3 \sqrt{3} y\right)\right) + \cos \left(\frac{2}{3} \pi \left(-8 x-2 \sqrt{3} y\right)\right) \\ & \qquad \qquad -\cos \left(\frac{2}{3} \pi \left(2 \sqrt{3} y-8 x\right)\right) -\cos \left(\frac{2}{3} \pi \left(7 x+3 \sqrt{3} y\right)\right) +\cos \left(\frac{2}{3} \pi \left(x+5 \sqrt{3} y\right)\right) \end{align*}
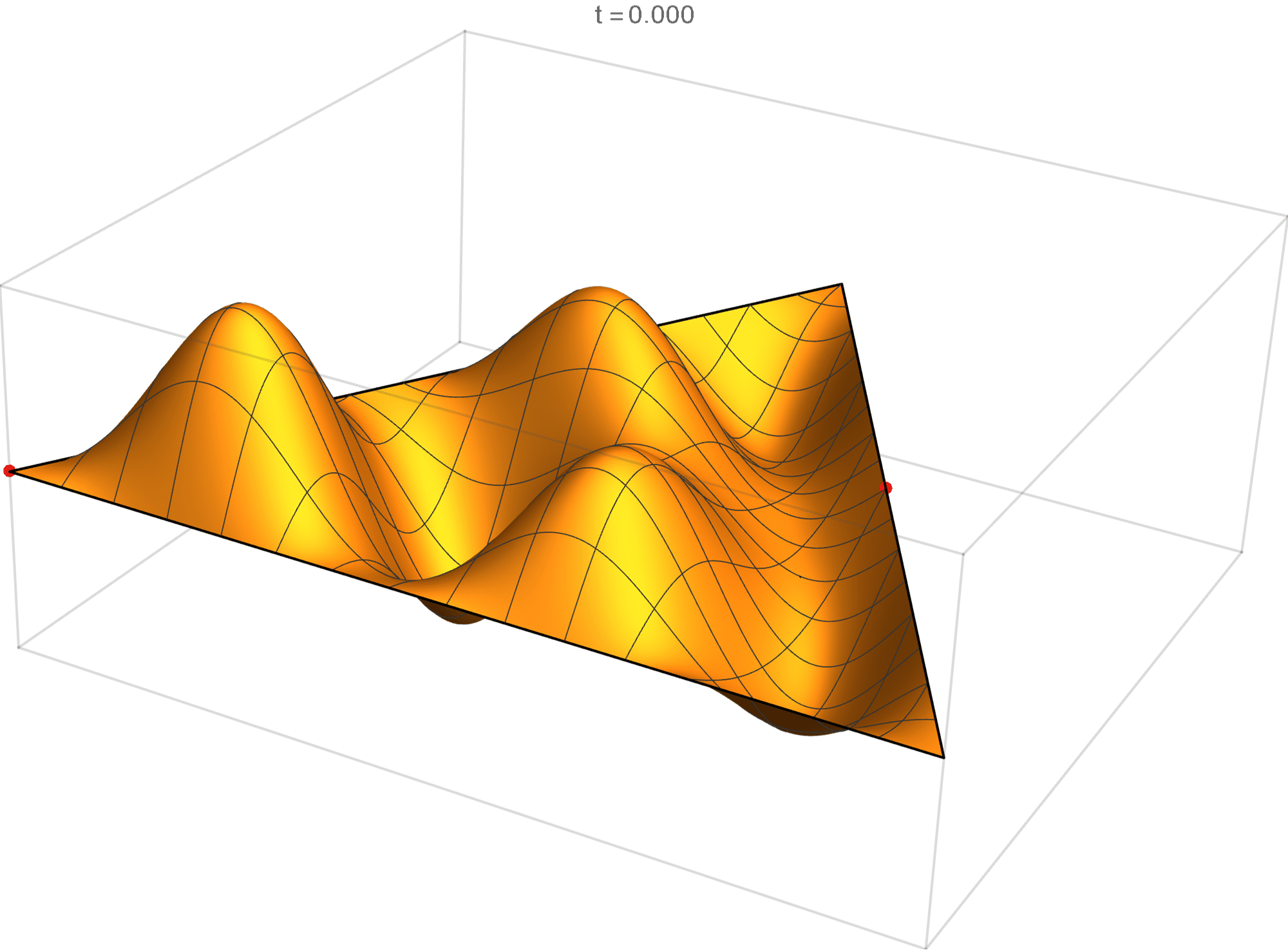
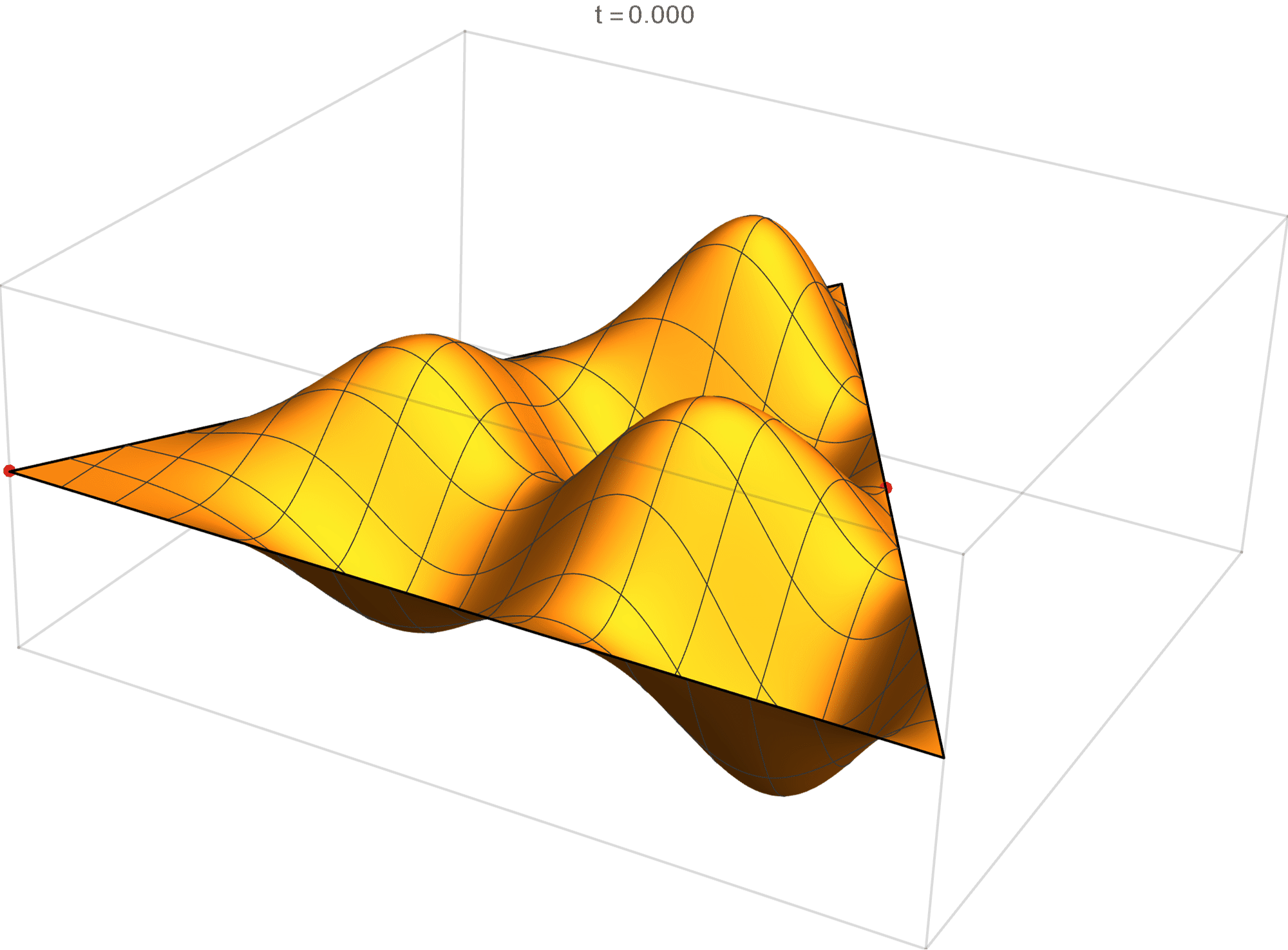
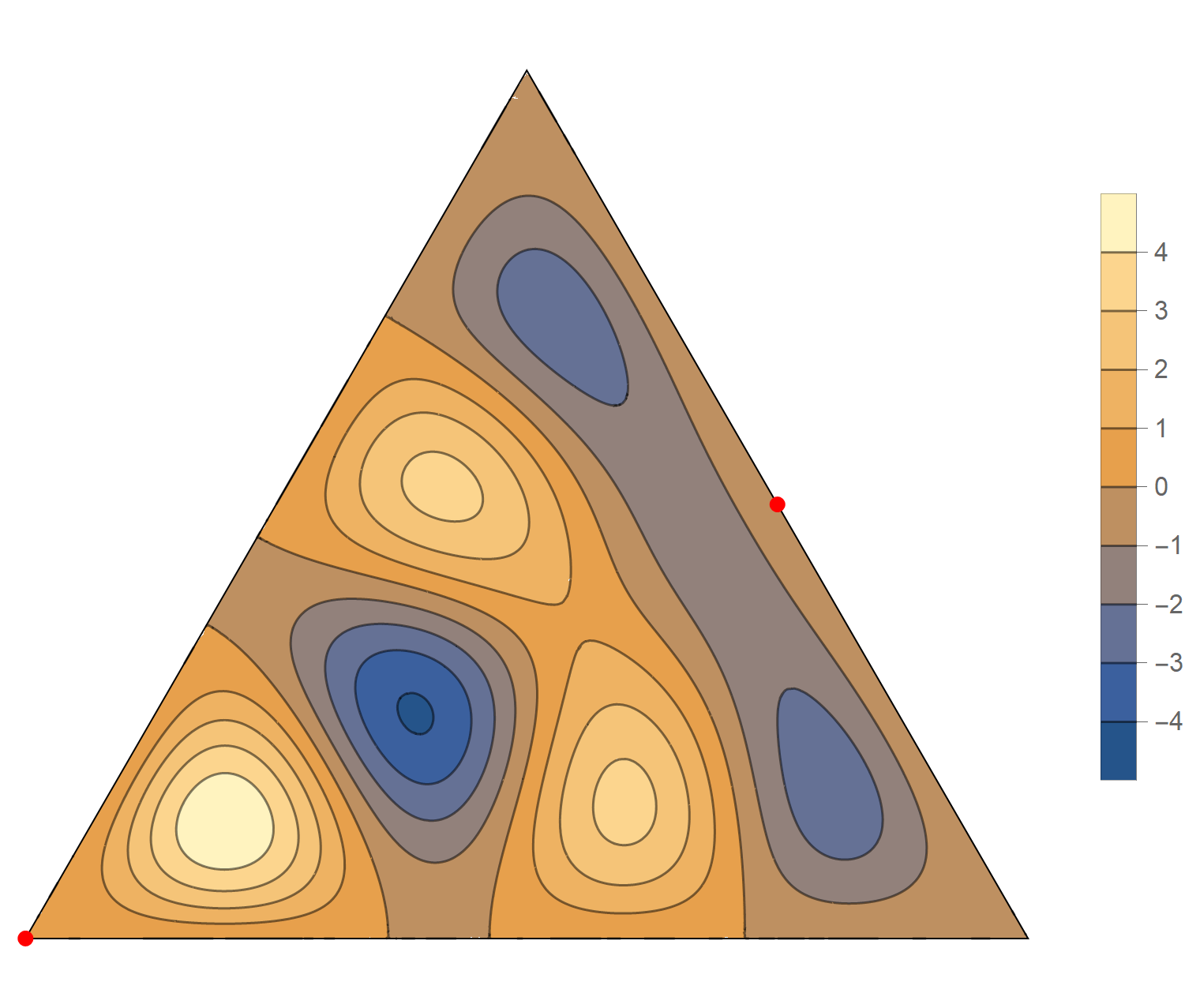
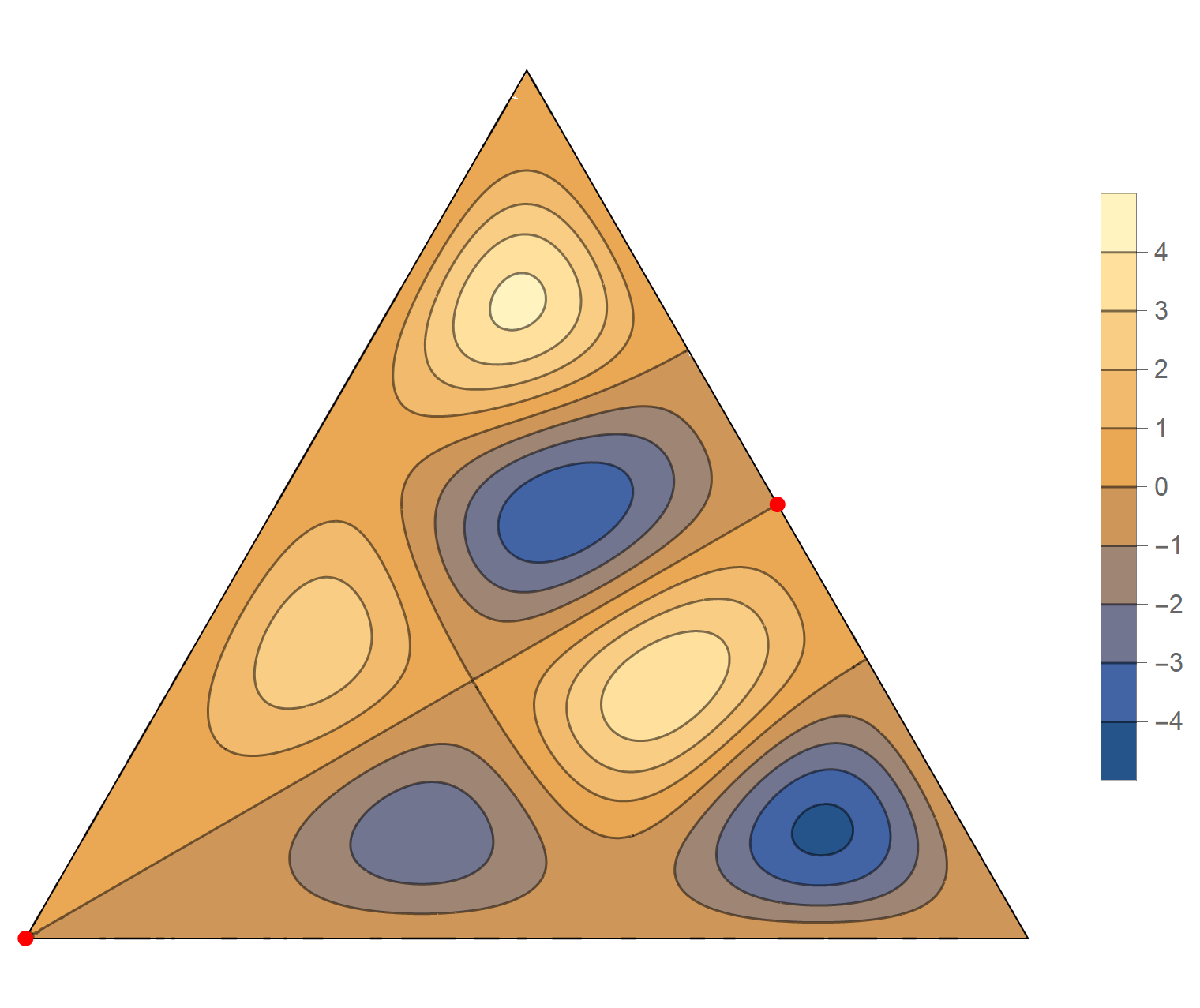
We review the entire two dimensional eigenspace as follows:
\[(\cos\theta)\operatorname{im}(x,y) +(\sin\theta) \operatorname{re}(x,y) \quad \text{as a function of} \quad \theta \in [0,2\pi).\]
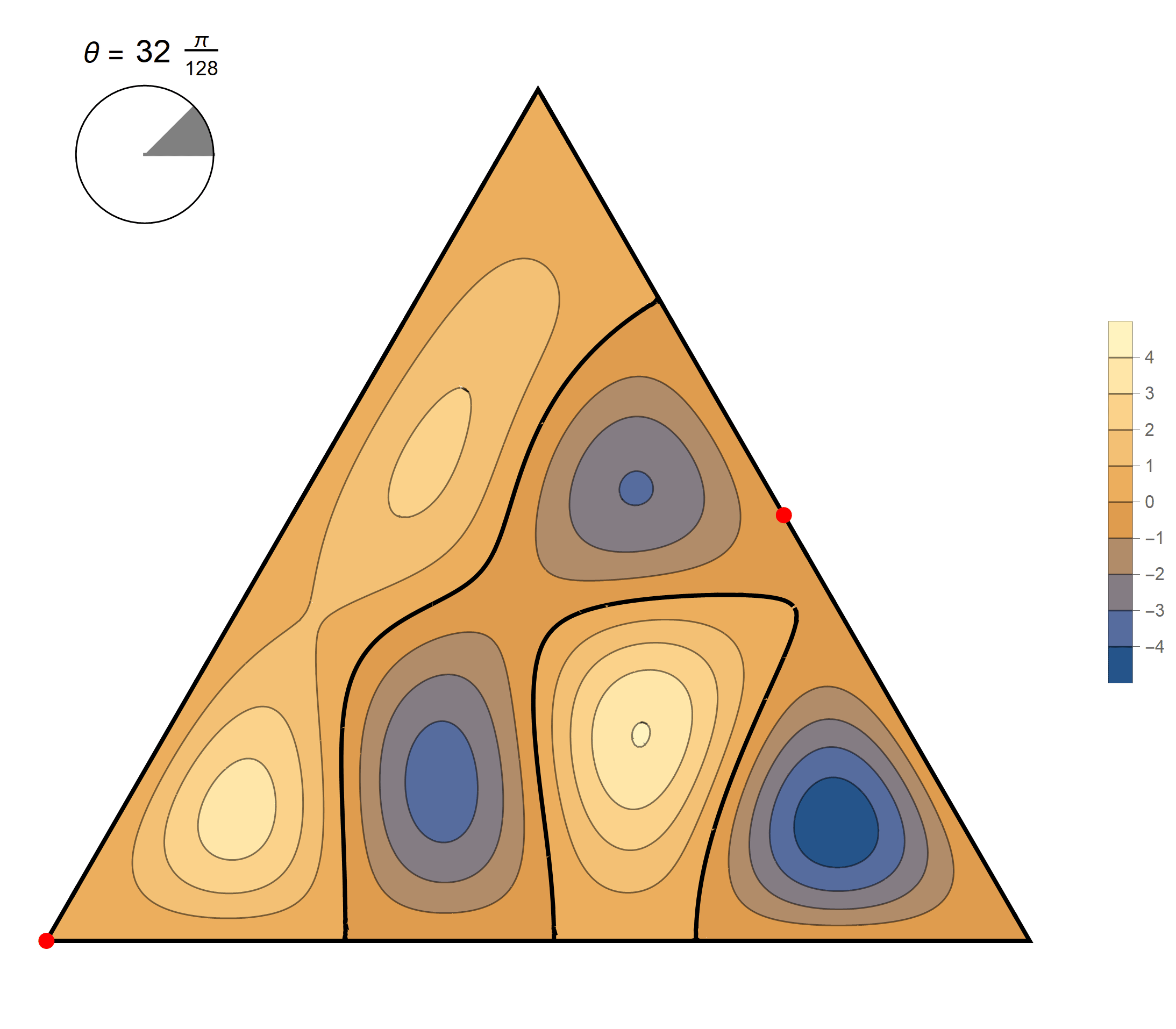
The sixth eigenvalue has multiplicity 2. The $(m,n)$ pairs that we used to construct the eigenfunction are \[ (6, 9), \quad (6, -3), \quad (-9, -3), \quad (-9, -6), \quad (3, -6), \quad (3, 9). \] The eigenfunctions are
\begin{align*} \operatorname{im}(x,y) & = -\sin \left(\frac{2}{3} \pi \left(3 x-5 \sqrt{3} y\right)\right) +\sin \left(\frac{2}{3} \pi \left(6 x-4 \sqrt{3} y\right)\right) +\sin \left(\frac{2}{3} \pi \left(-9 x-\sqrt{3} y\right)\right) \\ &\qquad\qquad -\sin\left(\frac{2}{3} \pi \left(\sqrt{3} y-9 x\right)\right)-\sin \left(\frac{2}{3} \pi \left(6 x+4 \sqrt{3} y\right)\right)+\sin \left(\frac{2}{3} \pi \left(3 x+5 \sqrt{3} y\right)\right) \\ \operatorname{re}(x,y) & = -\cos \left(\frac{2}{3} \pi \left(3 x-5 \sqrt{3} y\right)\right) +\cos \left(\frac{2}{3} \pi \left(6 x-4 \sqrt{3} y\right)\right) +\cos \left(\frac{2}{3} \pi \left(-9 x-\sqrt{3} y\right)\right) \\ &\qquad\qquad-\cos\left(\frac{2}{3} \pi \left(\sqrt{3} y-9 x\right)\right) -\cos \left(\frac{2}{3} \pi \left(6 x+4 \sqrt{3} y\right)\right)+\cos \left(\frac{2}{3} \pi \left(3 x+5 \sqrt{3} y\right)\right) \end{align*}
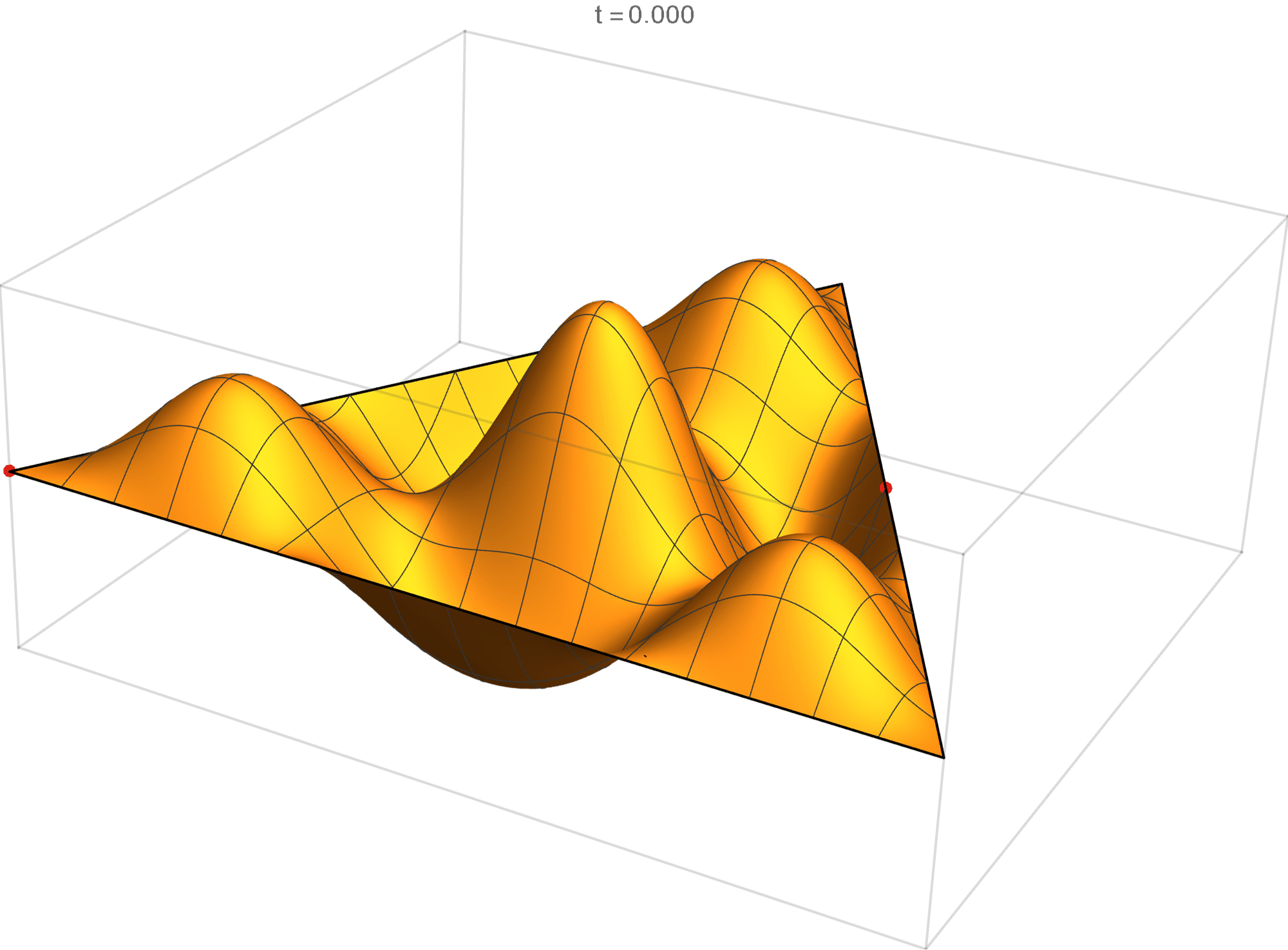
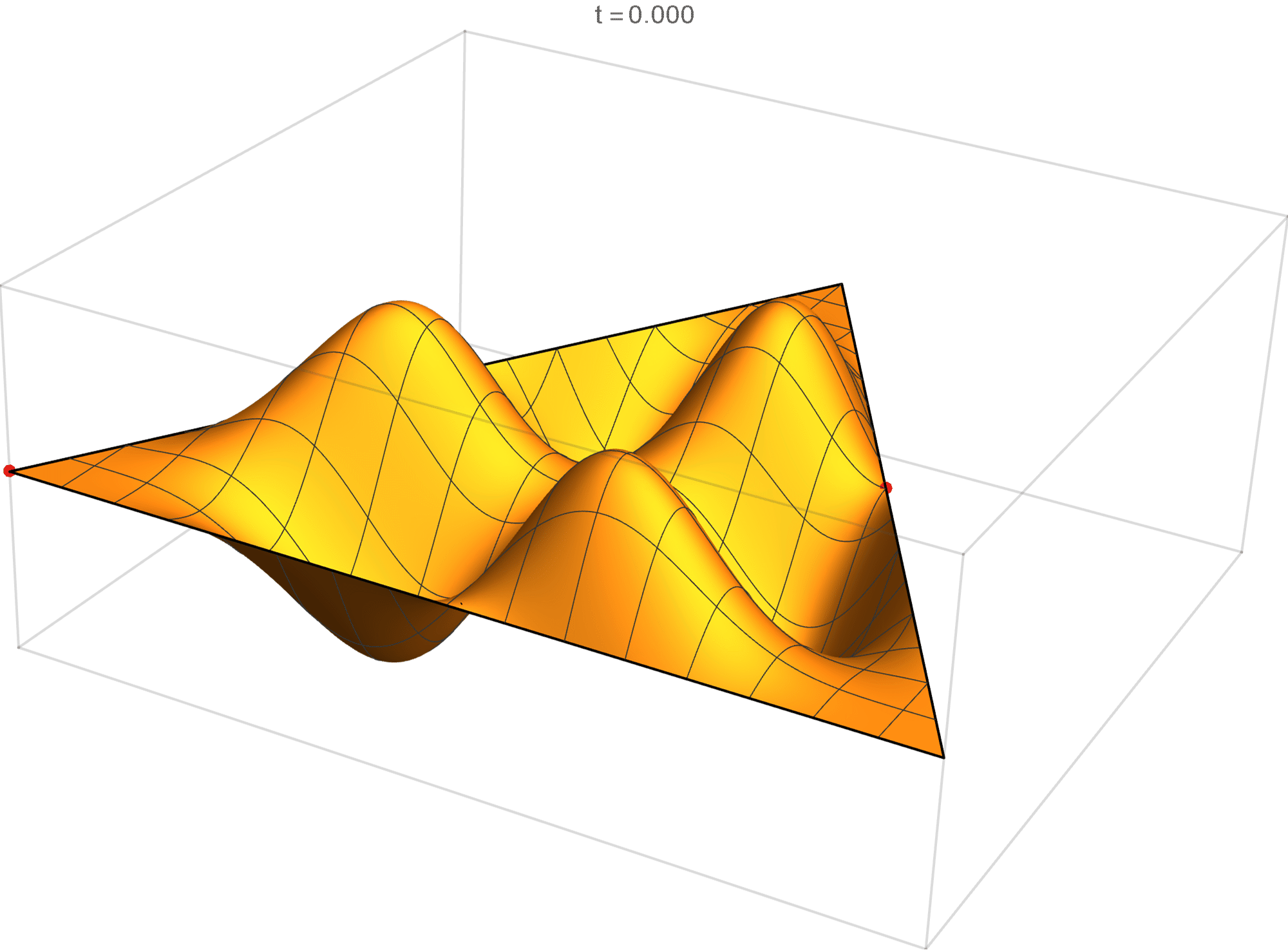
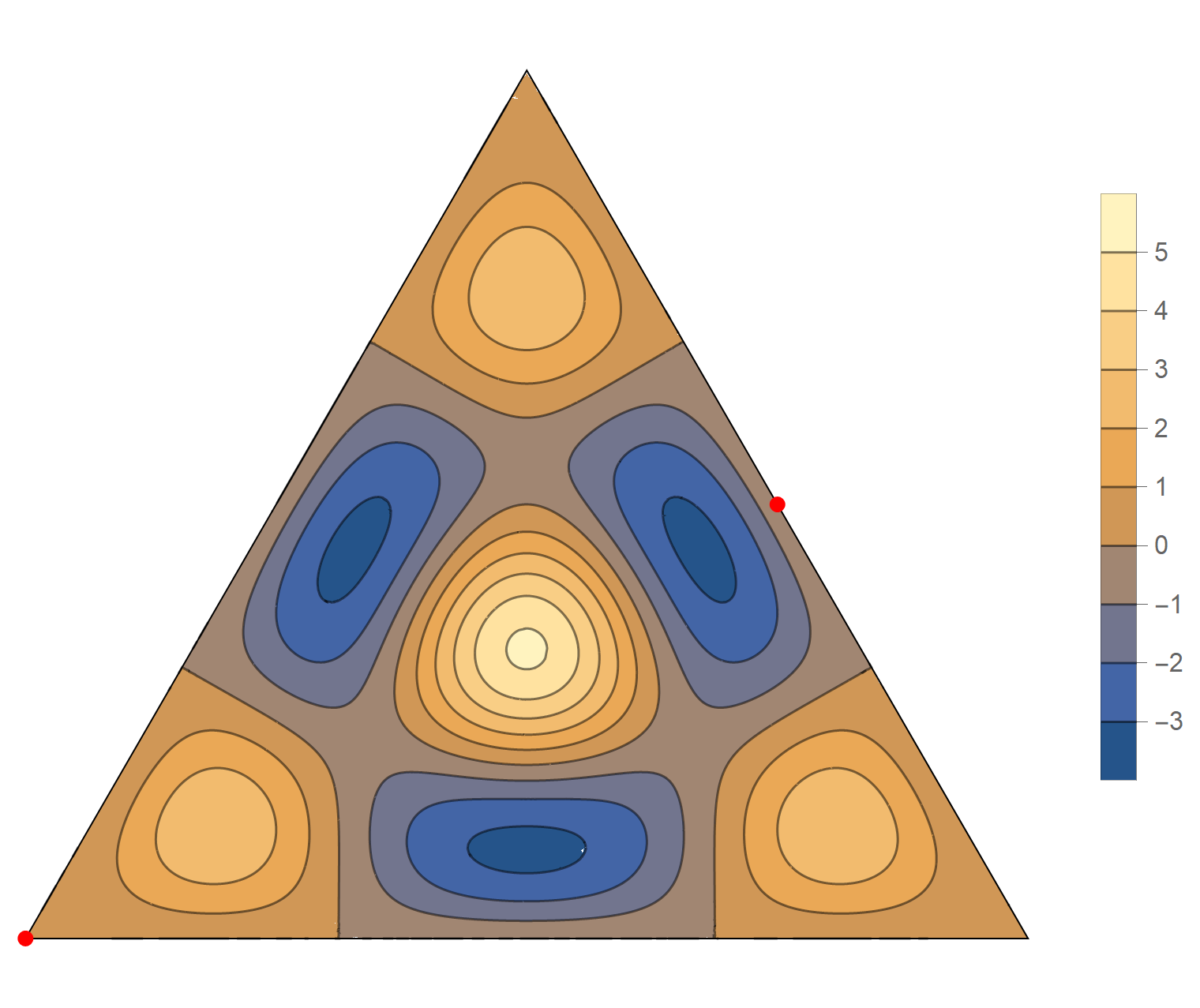
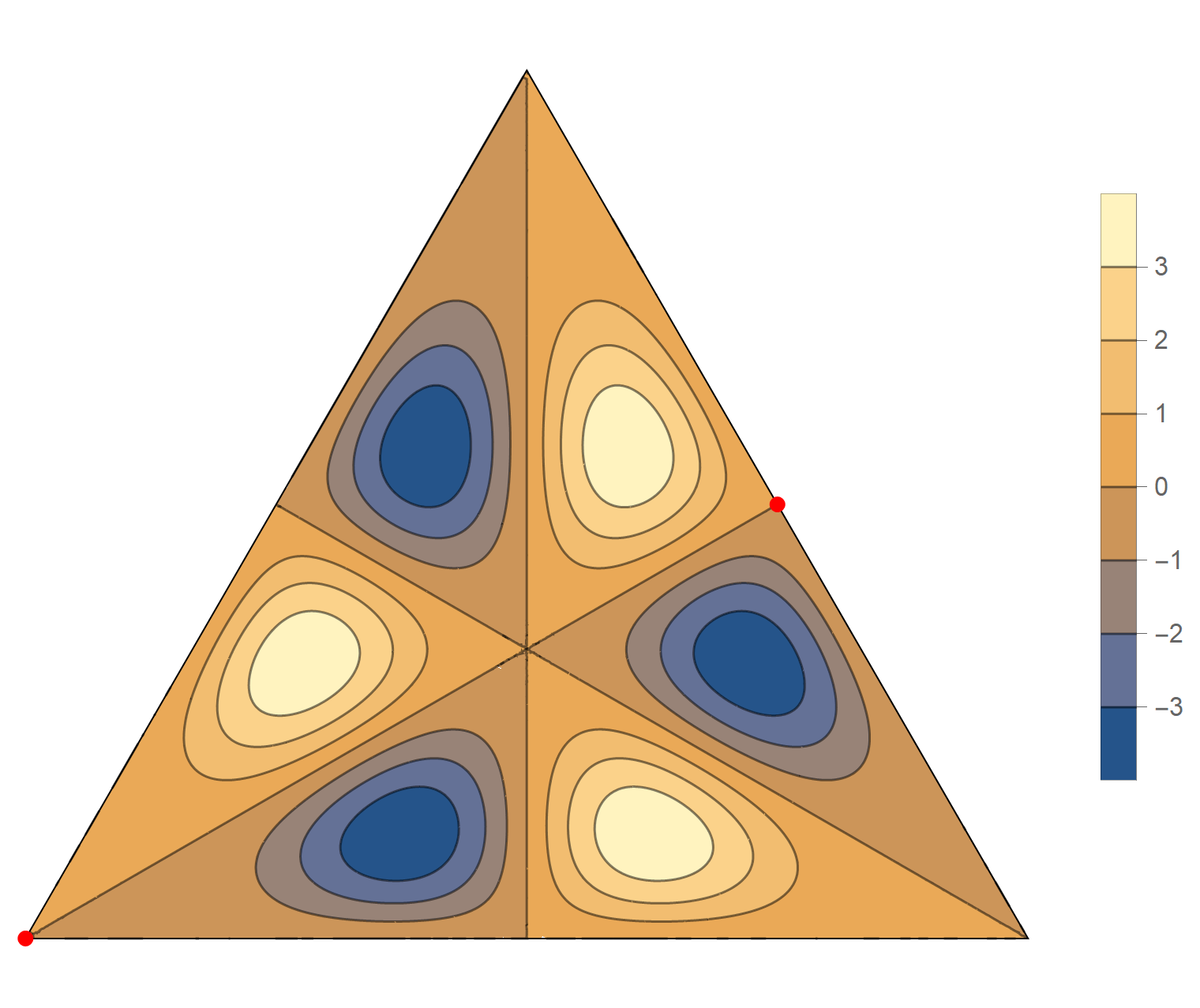
We review the entire two dimensional eigenspace as follows:
\[(\cos\theta)\operatorname{im}(x,y) +(\sin\theta) \operatorname{re}(x,y) \quad \text{as a function of} \quad \theta \in [0,2\pi).\]
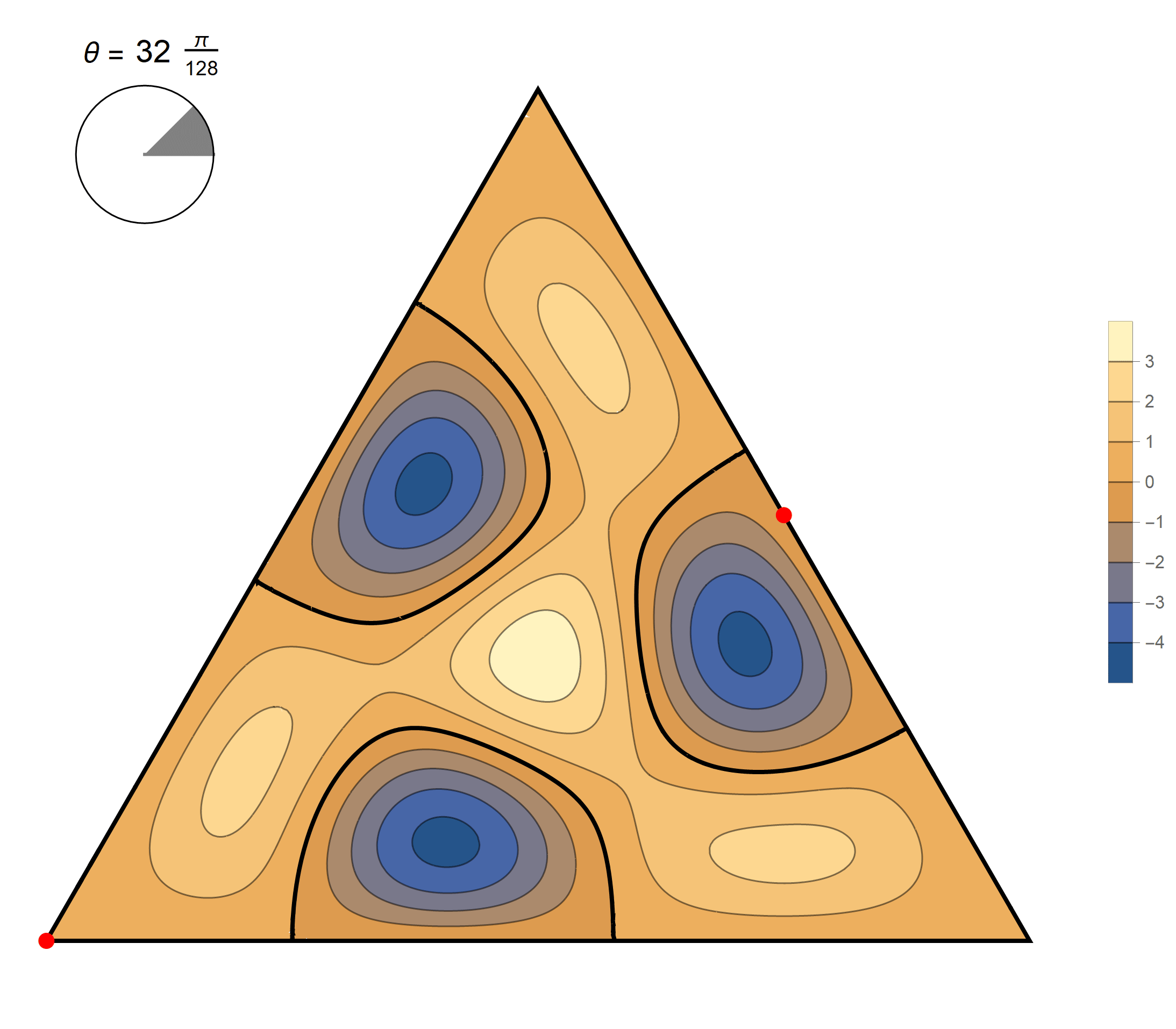
The seventh eigenvalue is simple. The $(m,n)$ pairs that we used to construct the eigenfunction are \[ (9, 9), \quad (9,0), \quad (-9,0), \quad (-9, -9), \quad (0,-9), \quad (0,9). \] The eigenfunctions are
\[ \operatorname{im}(x,y) = 2 \sin \left(\frac{2}{3} \pi \left(9 x-3 \sqrt{3} y\right)\right)-2 \sin \left(\frac{2}{3} \pi \left(9 x+3 \sqrt{3} y\right)\right)+2 \sin \left(4 \sqrt{3} \pi y\right) \]
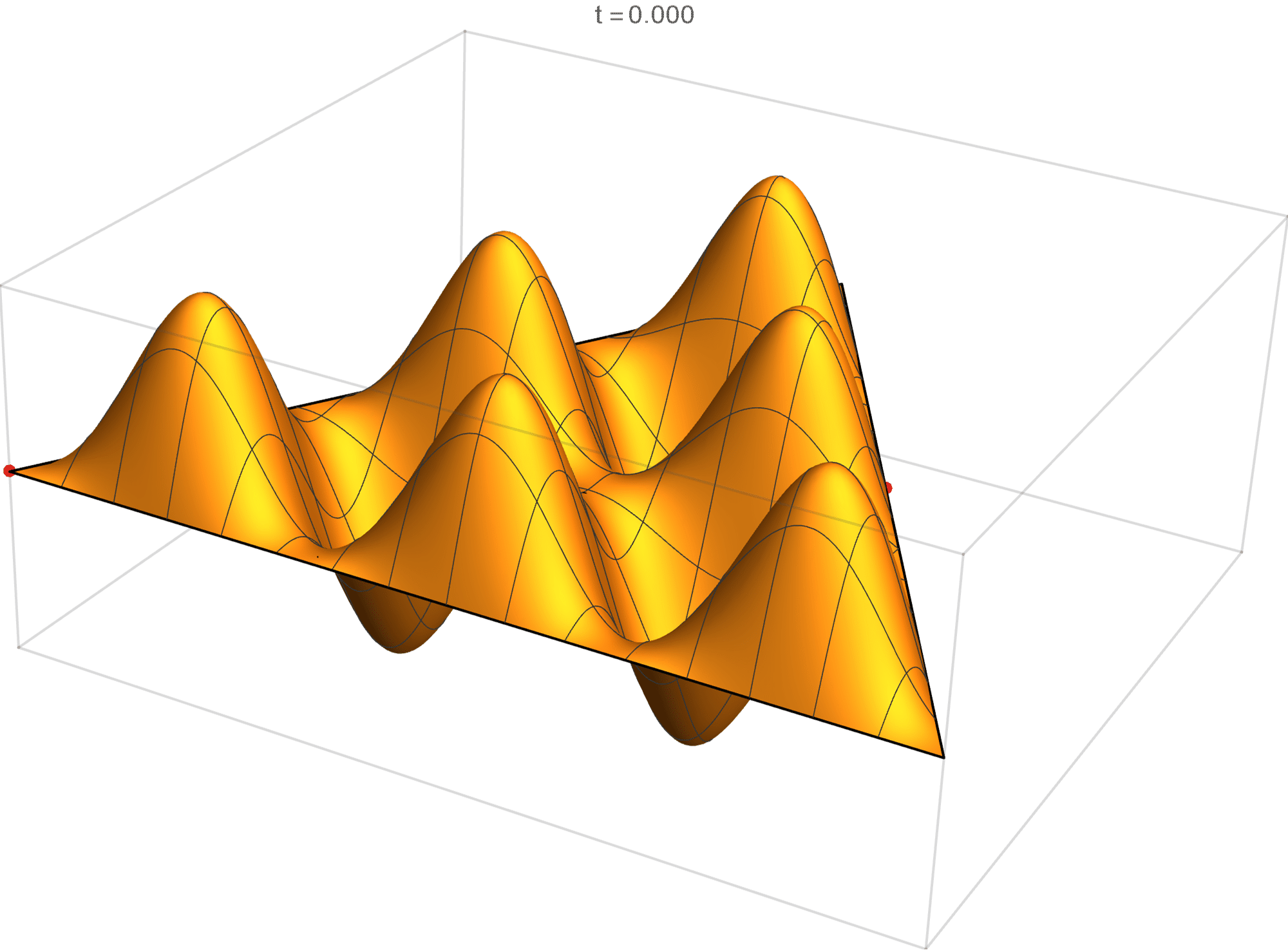
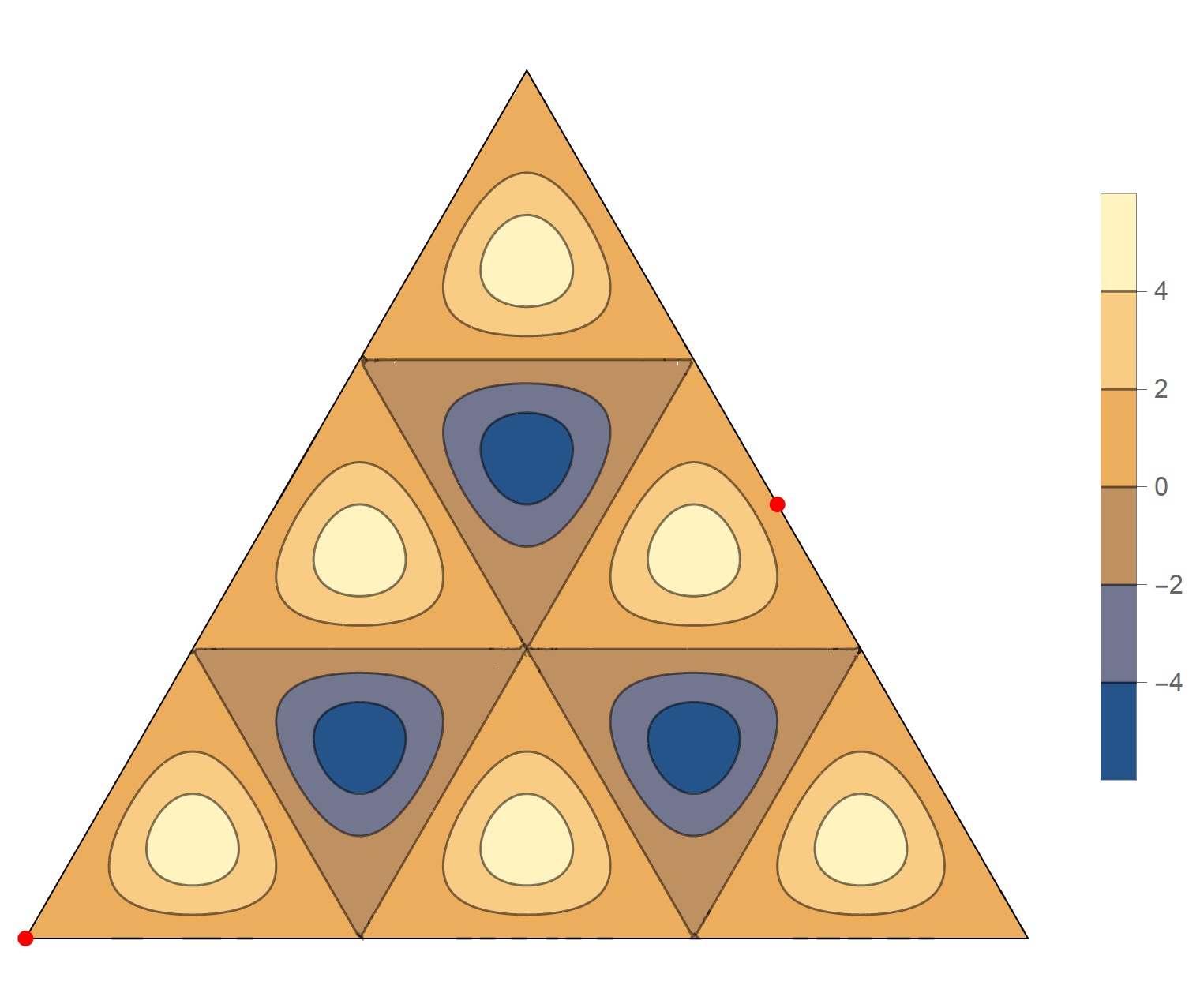
The eighth eigenvalue has multiplicity 2. The $(m,n)$ pairs that we used to construct the eigenfunction are \[ (8, 10), \quad (8,-2), \quad (-10, -2), \quad (-10, -8), \quad (2, -8), \quad (2, 10). \] The eigenfunctions are
\begin{align*} \operatorname{im}(x,y) & = -\sin \left(\frac{2}{3} \pi \left(2 x-6 \sqrt{3} y\right)\right) +\sin \left(\frac{2}{3} \pi \left(8 x-4\sqrt{3} y\right)\right) +\sin \left(\frac{2}{3} \pi \left(-10 x-2 \sqrt{3} y\right)\right)\\ & \qquad\qquad-\sin \left(\frac{2}{3} \pi \left(2 \sqrt{3} y-10 x\right)\right)-\sin \left(\frac{2}{3} \pi \left(8 x+4 \sqrt{3} y\right)\right)+\sin \left(\frac{2}{3} \pi \left(2 x+6 \sqrt{3} y\right)\right) \\ \operatorname{re}(x,y) & =-\cos \left(\frac{2}{3} \pi \left(2 x-6 \sqrt{3} y\right)\right) +\cos \left(\frac{2}{3} \pi \left(8 x-4 \sqrt{3} y\right)\right) +\cos \left(\frac{2}{3} \pi \left(-10 x-2 \sqrt{3} y\right)\right)\\ &\qquad\qquad-\cos\left(\frac{2}{3} \pi \left(2 \sqrt{3} y-10 x\right)\right)-\cos \left(\frac{2}{3} \pi \left(8 x+4 \sqrt{3} y\right)\right)+\cos \left(\frac{2}{3} \pi \left(2 x+6 \sqrt{3} y\right)\right) \end{align*}
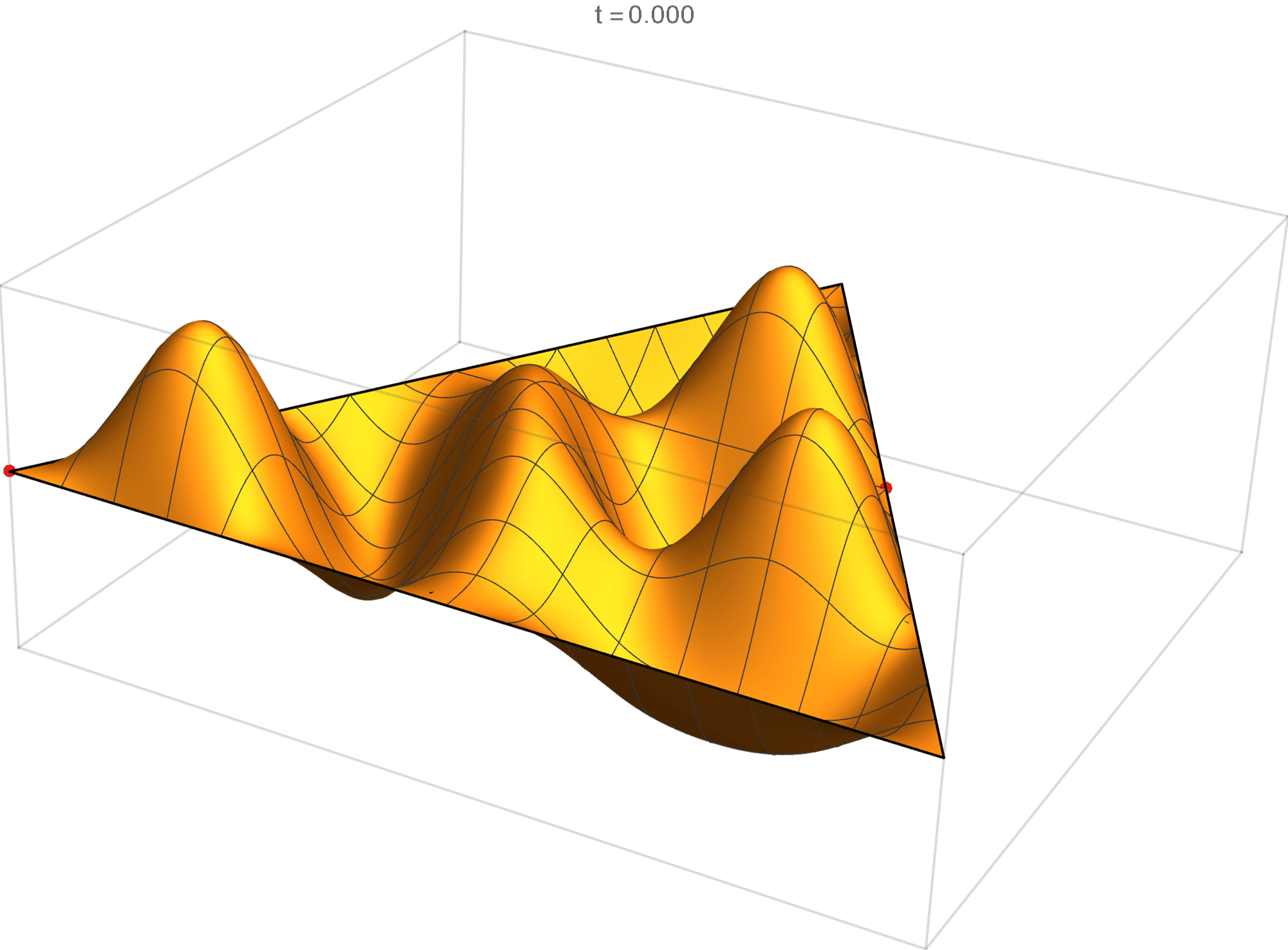
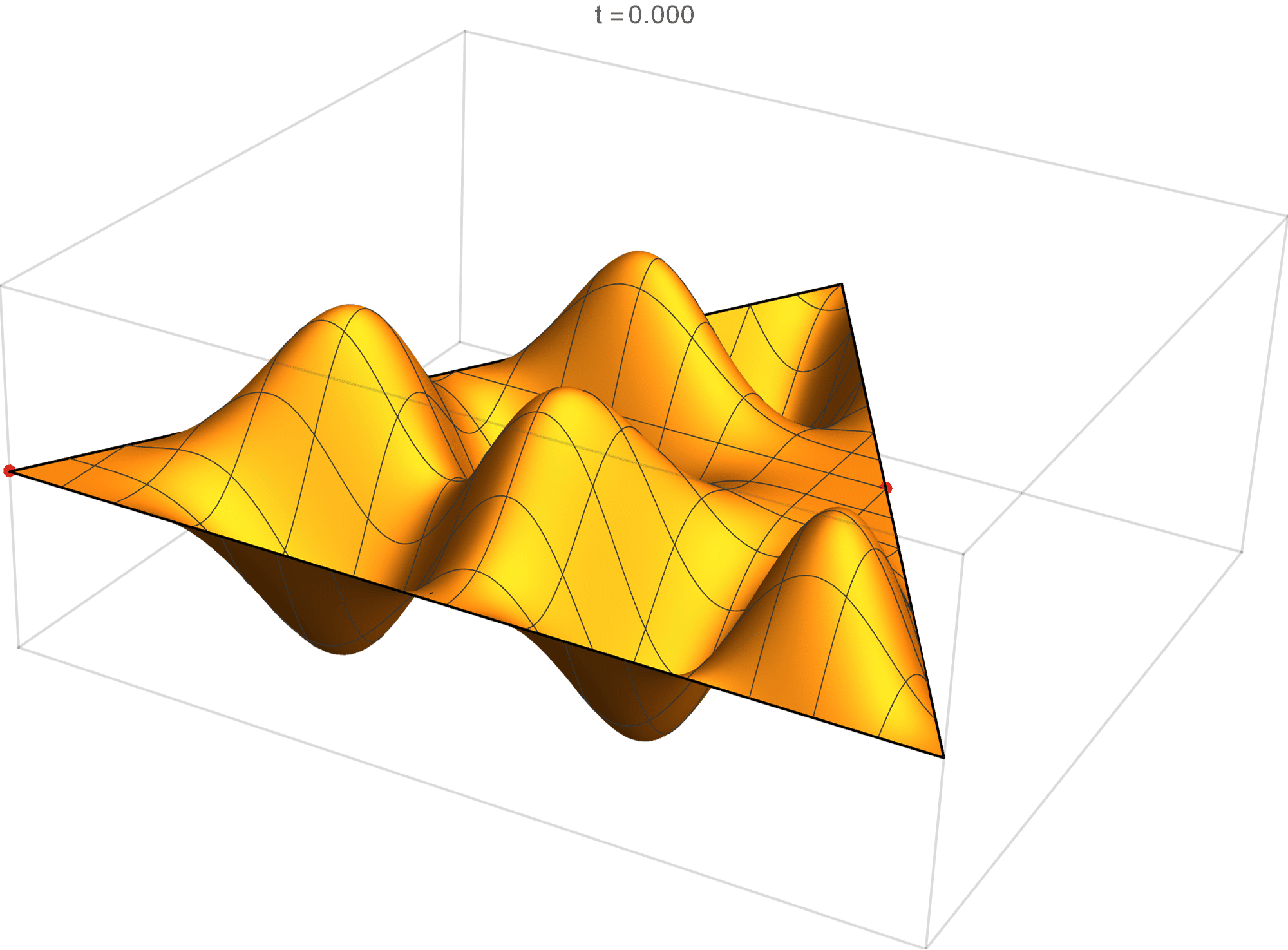
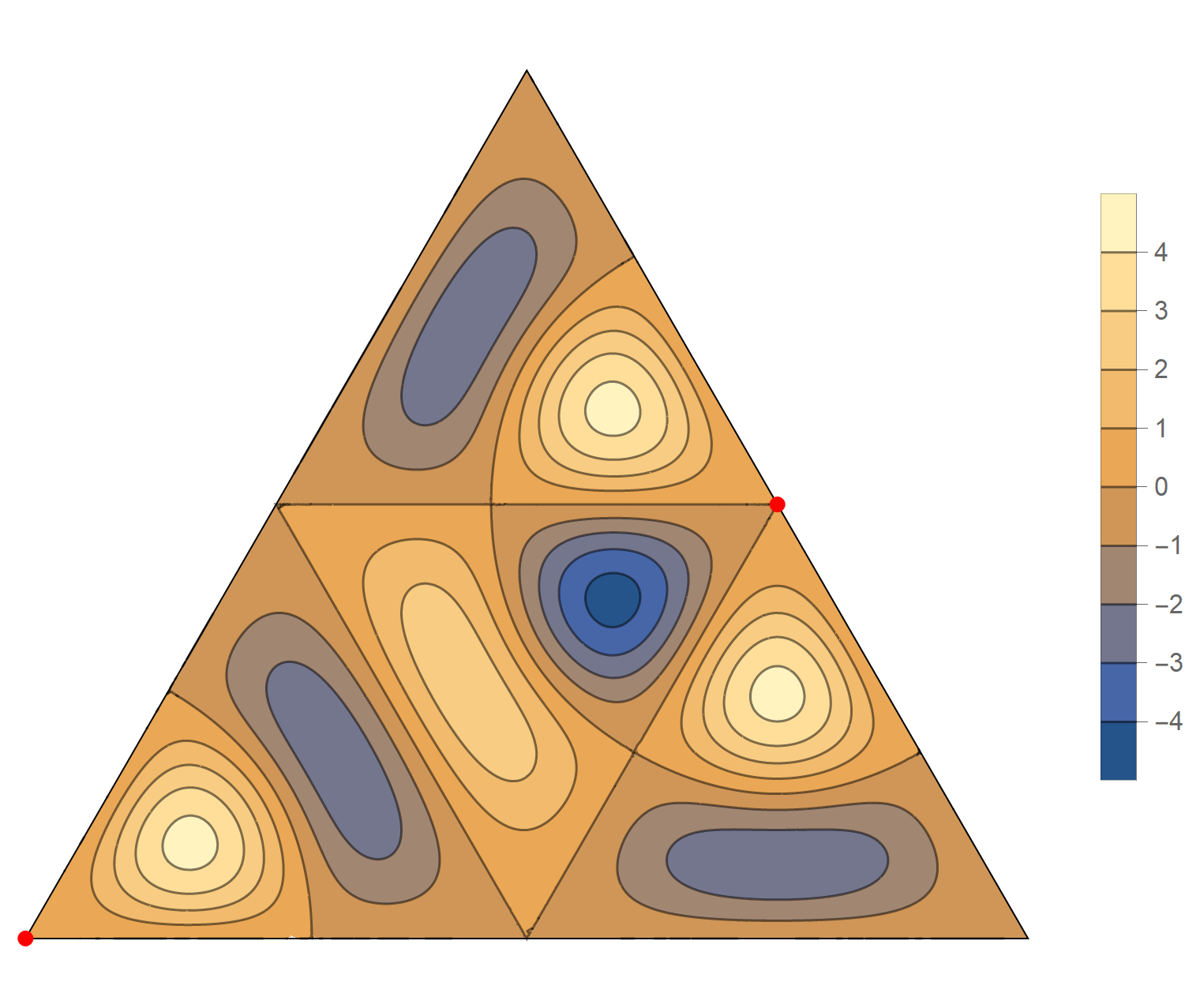
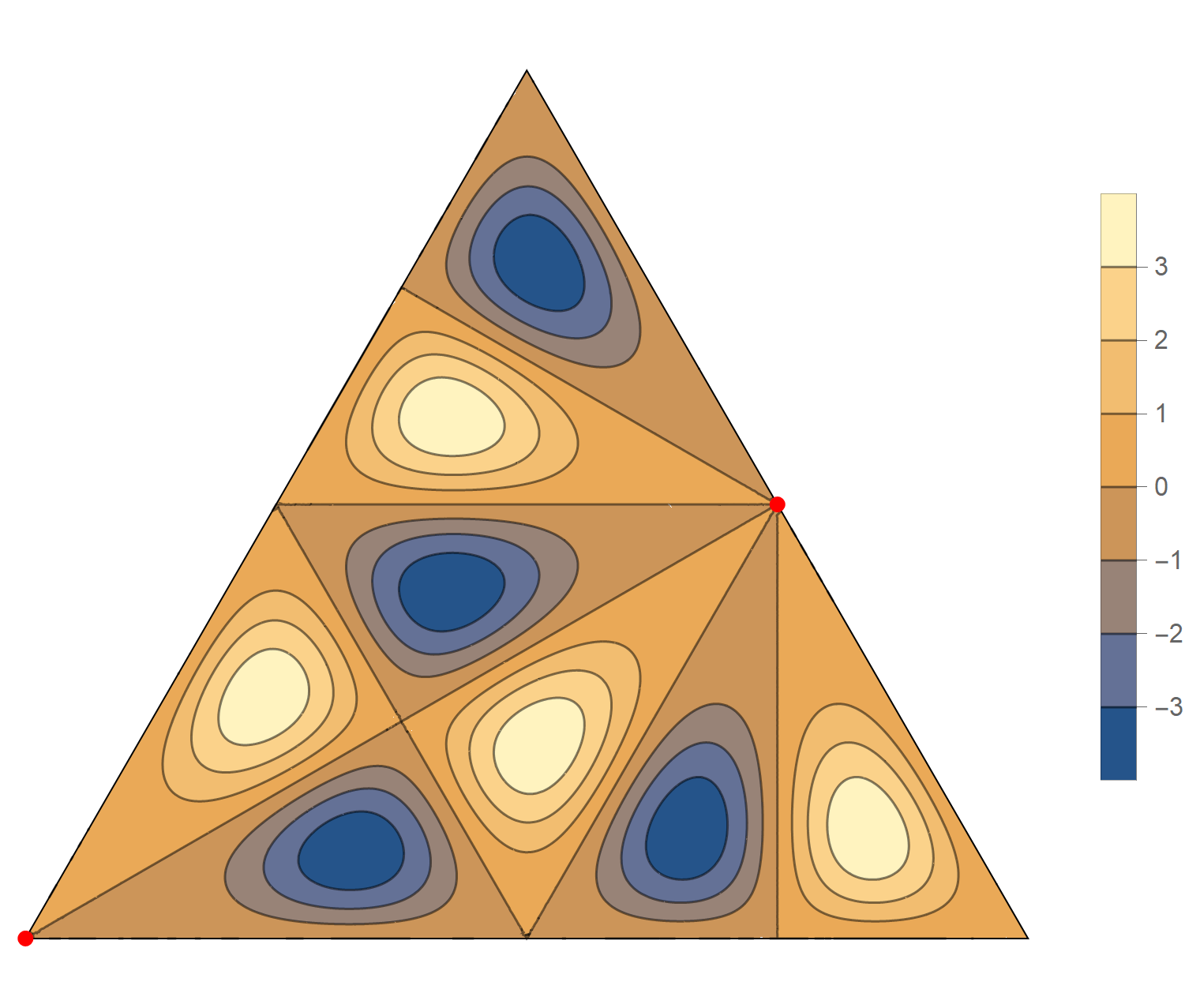
We review the entire two dimensional eigenspace as follows:
\[(\cos\theta)\operatorname{im}(x,y) +(\sin\theta) \operatorname{re}(x,y) \quad \text{as a function of} \quad \theta \in [0,2\pi).\]
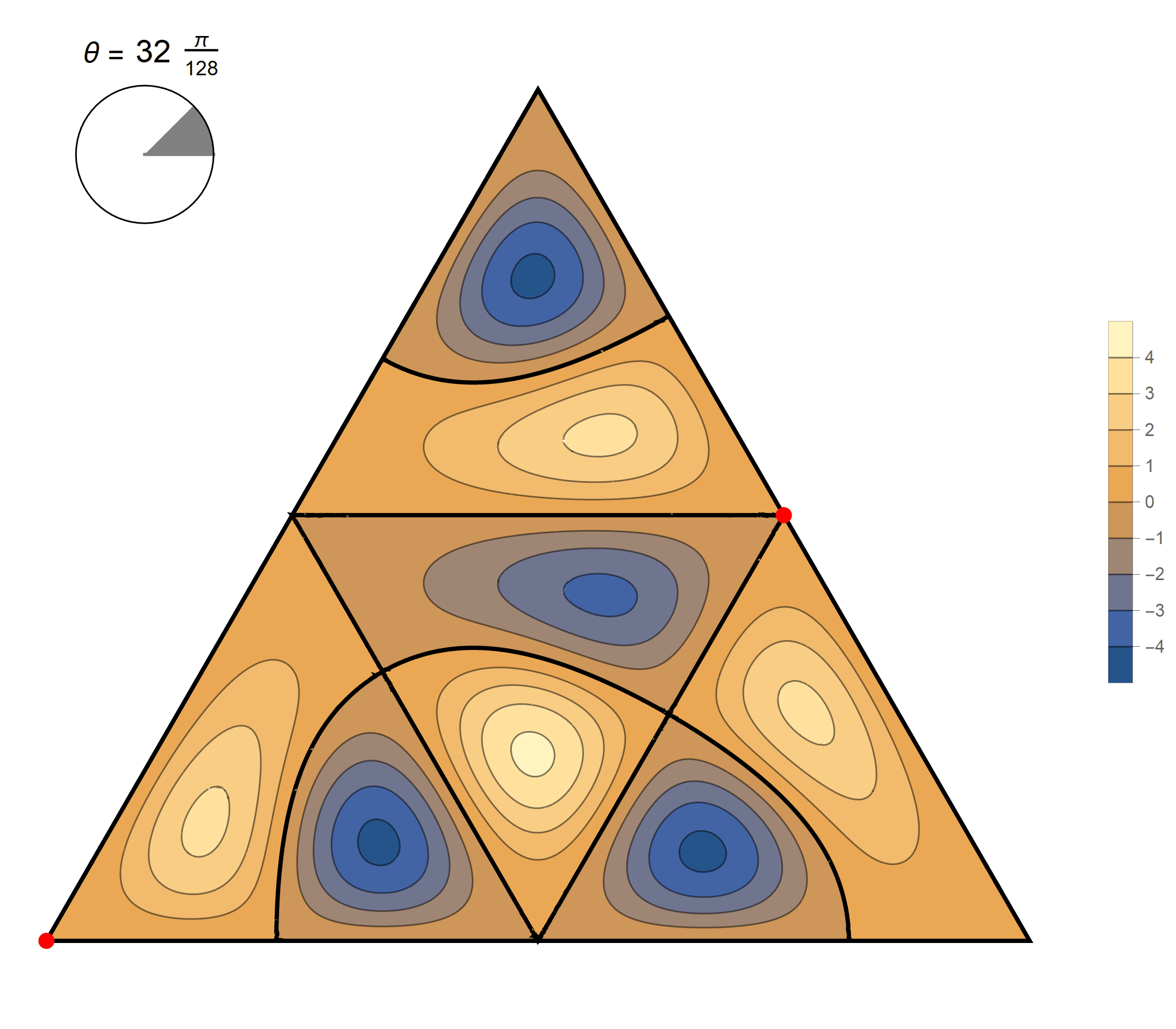
The nineth eigenvalue has multiplicity 2. The $(m,n)$ pairs that we used to construct the eigenfunction are \[ (7, 11), \quad (7, -4), \quad (-11, -4), \quad (-11, -7), \quad (4, -7), \quad (4, 11). \] The eigenfunctions are
\begin{align*} \operatorname{im}(x,y) & = -\sin \left(\frac{2}{3} \pi \left(4 x-6 \sqrt{3} y\right)\right) +\sin \left(\frac{2}{3} \pi \left(7 x-5 \sqrt{3} y\right)\right) +\sin \left(\frac{2}{3} \pi \left(-11 x-\sqrt{3} y\right)\right) \\ & \qquad\qquad -\sin \left(\frac{2}{3} \pi \left(\sqrt{3} y-11 x\right)\right) -\sin \left(\frac{2}{3} \pi \left(7 x+5 \sqrt{3} y\right)\right)+\sin \left(\frac{2}{3} \pi \left(4 x+6 \sqrt{3} y\right)\right) \\ \operatorname{re}(x,y) & =-\cos \left(\frac{2}{3} \pi \left(4 x-6 \sqrt{3} y\right)\right) +\cos \left(\frac{2}{3} \pi \left(7 x-5 \sqrt{3} y\right)\right)+\cos \left(\frac{2}{3} \pi \left(-11 x-\sqrt{3} y\right)\right)\\ &\qquad\qquad-\cos \left(\frac{2}{3} \pi \left(\sqrt{3} y-11 x\right)\right)-\cos \left(\frac{2}{3} \pi \left(7 x+5 \sqrt{3} y\right)\right)+\cos \left(\frac{2}{3} \pi \left(4 x+6 \sqrt{3} y\right)\right) \end{align*}
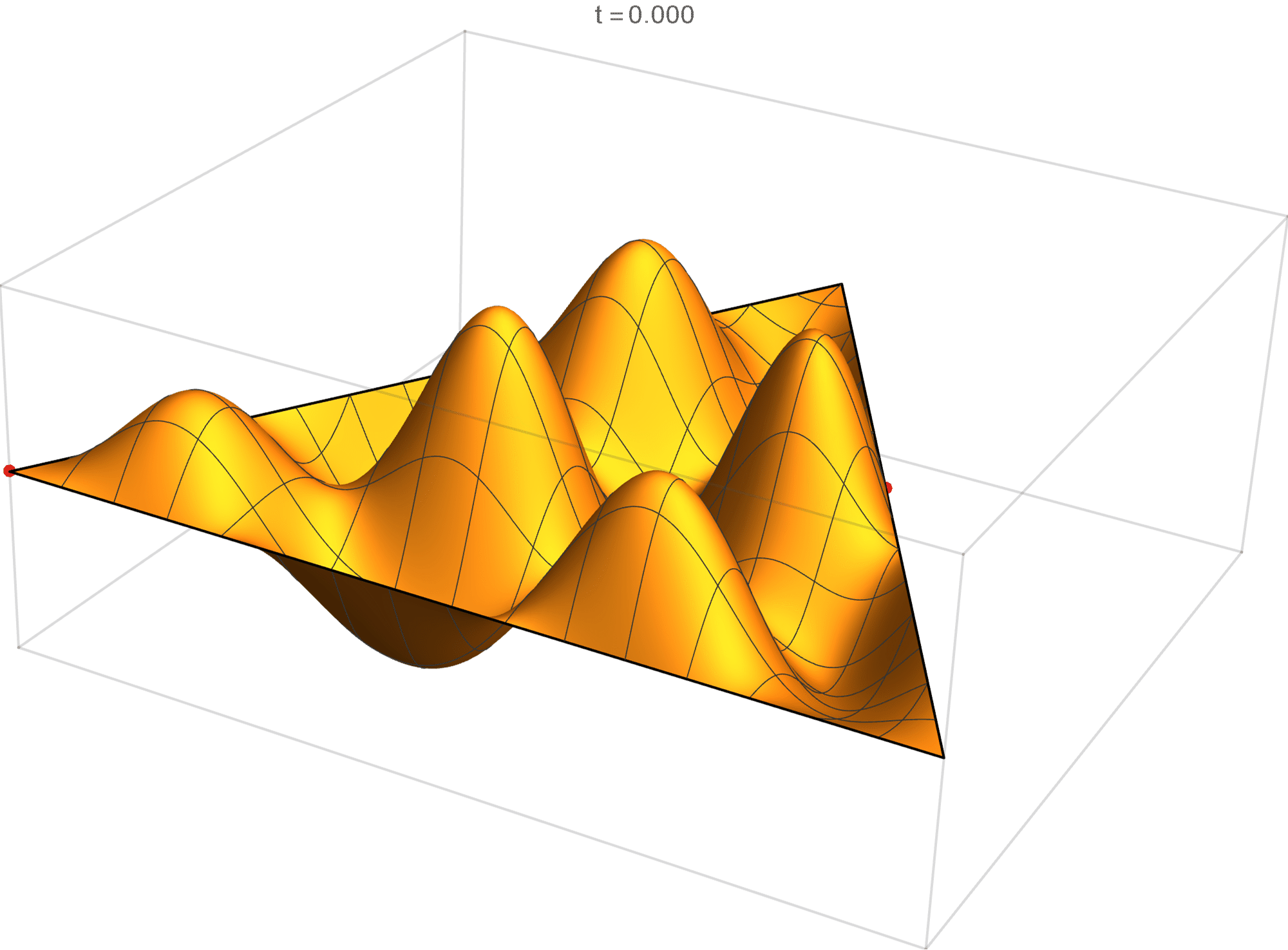
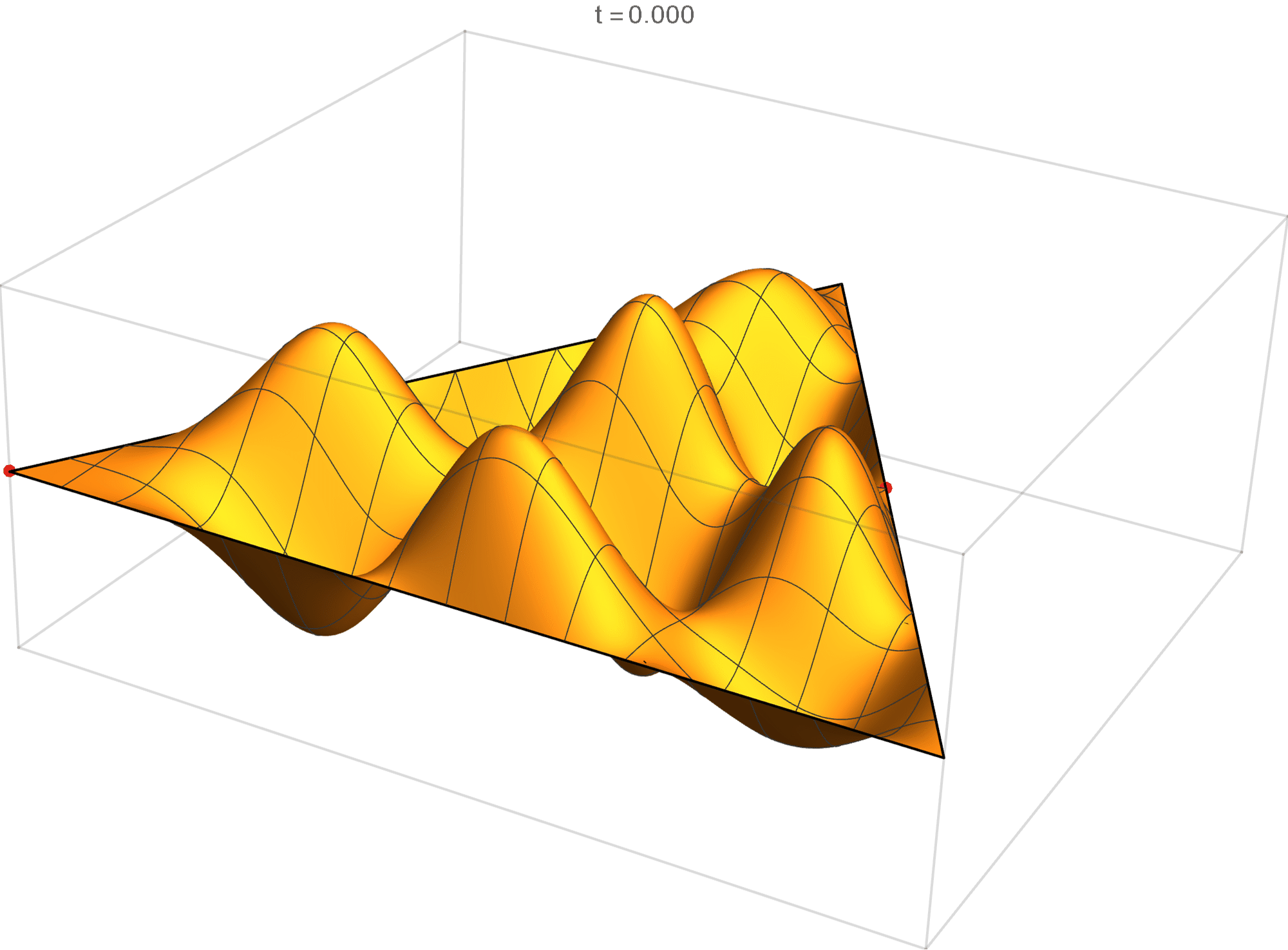
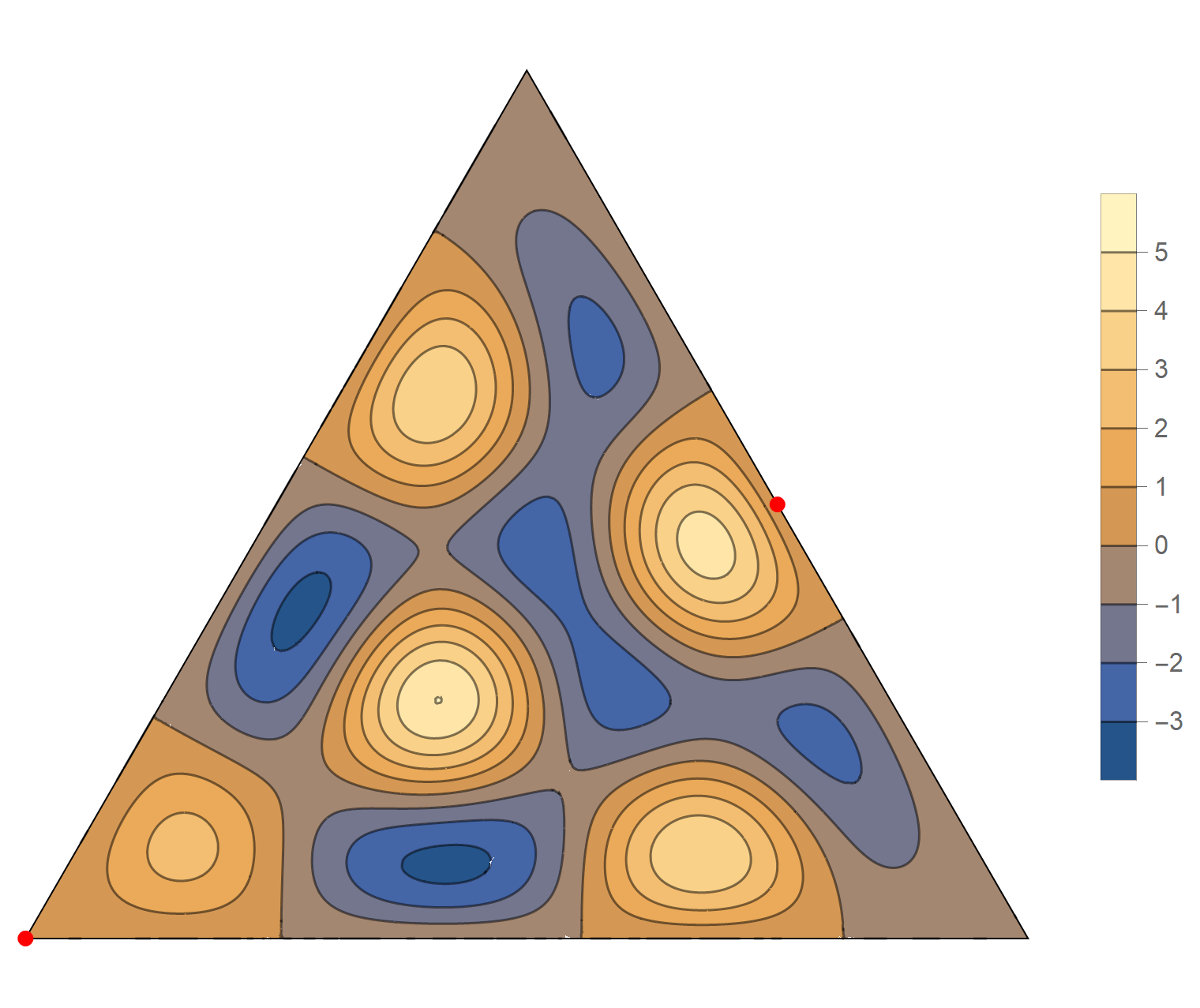
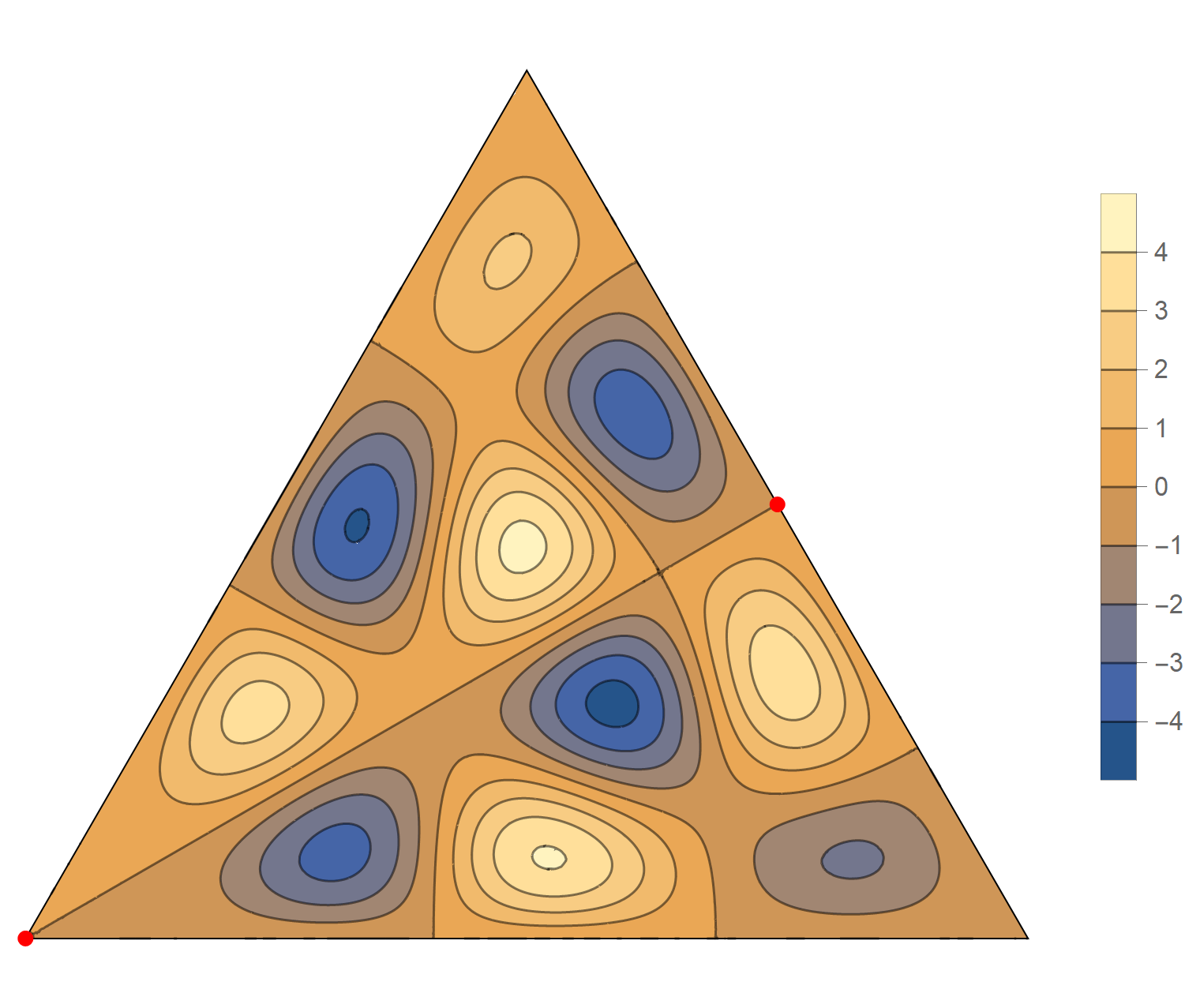
We review the entire two dimensional eigenspace as follows:
\[(\cos\theta)\operatorname{im}(x,y) +(\sin\theta) \operatorname{re}(x,y) \quad \text{as a function of} \quad \theta \in [0,2\pi).\]
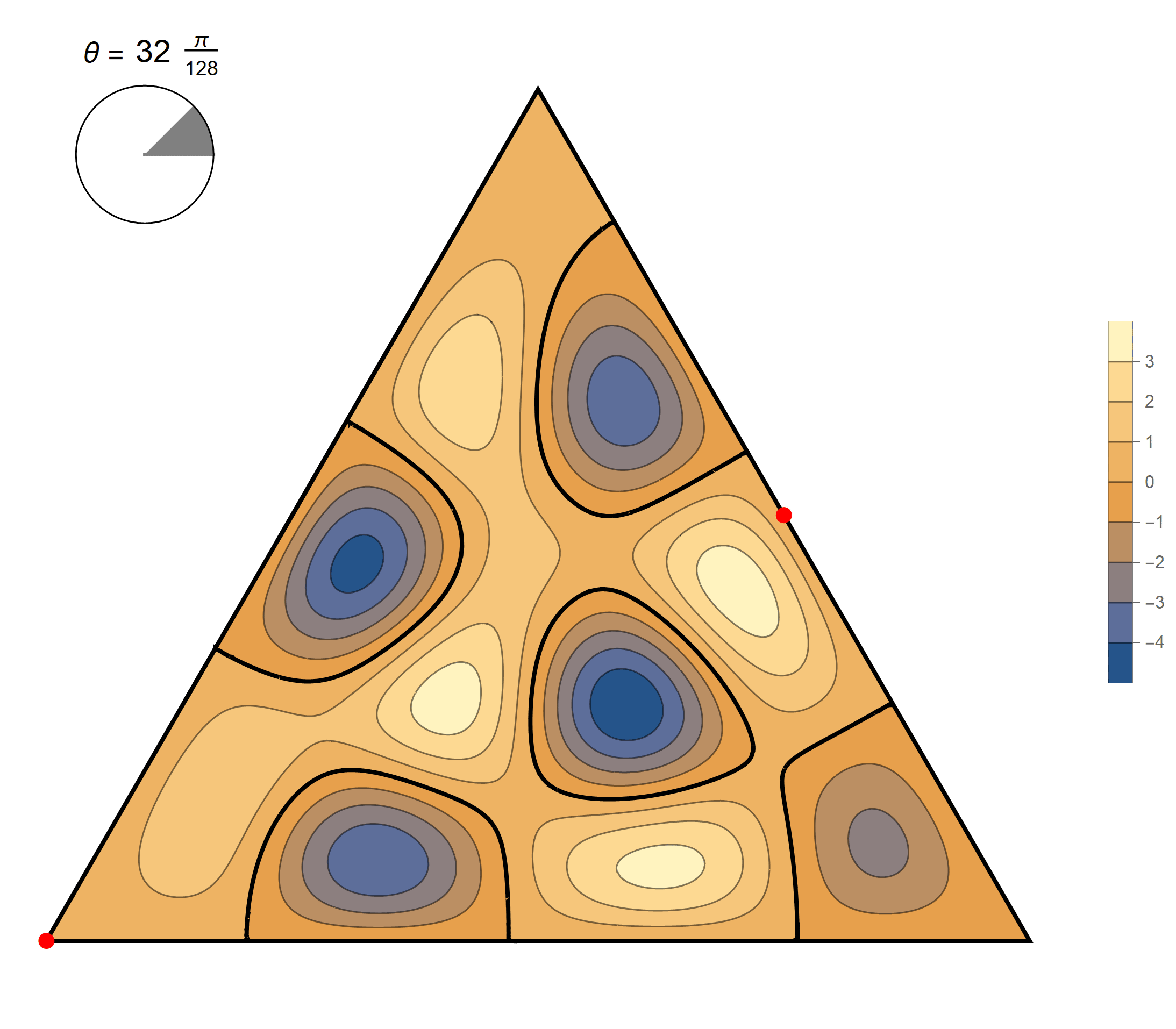
The tenth eigenvalue has multiplicity 2. The $(m,n)$ pairs that we used to construct the eigenfunction are \[ (10, 11), \quad (10, -1), \quad (-11, -1), \quad (-11, -10), \quad (1, -10), \quad (1,11). \] The eigenfunctions are
\begin{align*} \operatorname{im}(x,y) & = -\sin \left(\frac{2}{3} \pi \left(x-7 \sqrt{3} y\right)\right)+\sin \left(\frac{2}{3} \pi \left(10 x-4 \sqrt{3} y\right)\right)+\sin \left(\frac{2}{3} \pi \left(-11 x-3 \sqrt{3} y\right)\right)\\ &\qquad\qquad -\sin \left(\frac{2}{3} \pi \left(3 \sqrt{3} y-11 x\right)\right)-\sin \left(\frac{2}{3} \pi \left(10 x+4 \sqrt{3} y\right)\right)+\sin \left(\frac{2}{3} \pi \left(x+7 \sqrt{3} y\right)\right) \\ \operatorname{re}(x,y) & =-\cos \left(\frac{2}{3} \pi \left(x-7 \sqrt{3} y\right)\right)+\cos \left(\frac{2}{3} \pi \left(10 x-4 \sqrt{3} y\right)\right)+\cos \left(\frac{2}{3} \pi \left(-11 x-3 \sqrt{3} y\right)\right)\\ &\qquad\qquad-\cos \left(\frac{2}{3} \pi \left(3 \sqrt{3} y-11 x\right)\right)-\cos \left(\frac{2}{3} \pi \left(10 x+4 \sqrt{3} y\right)\right)+\cos \left(\frac{2}{3} \pi \left(x+7 \sqrt{3} y\right)\right) \end{align*}
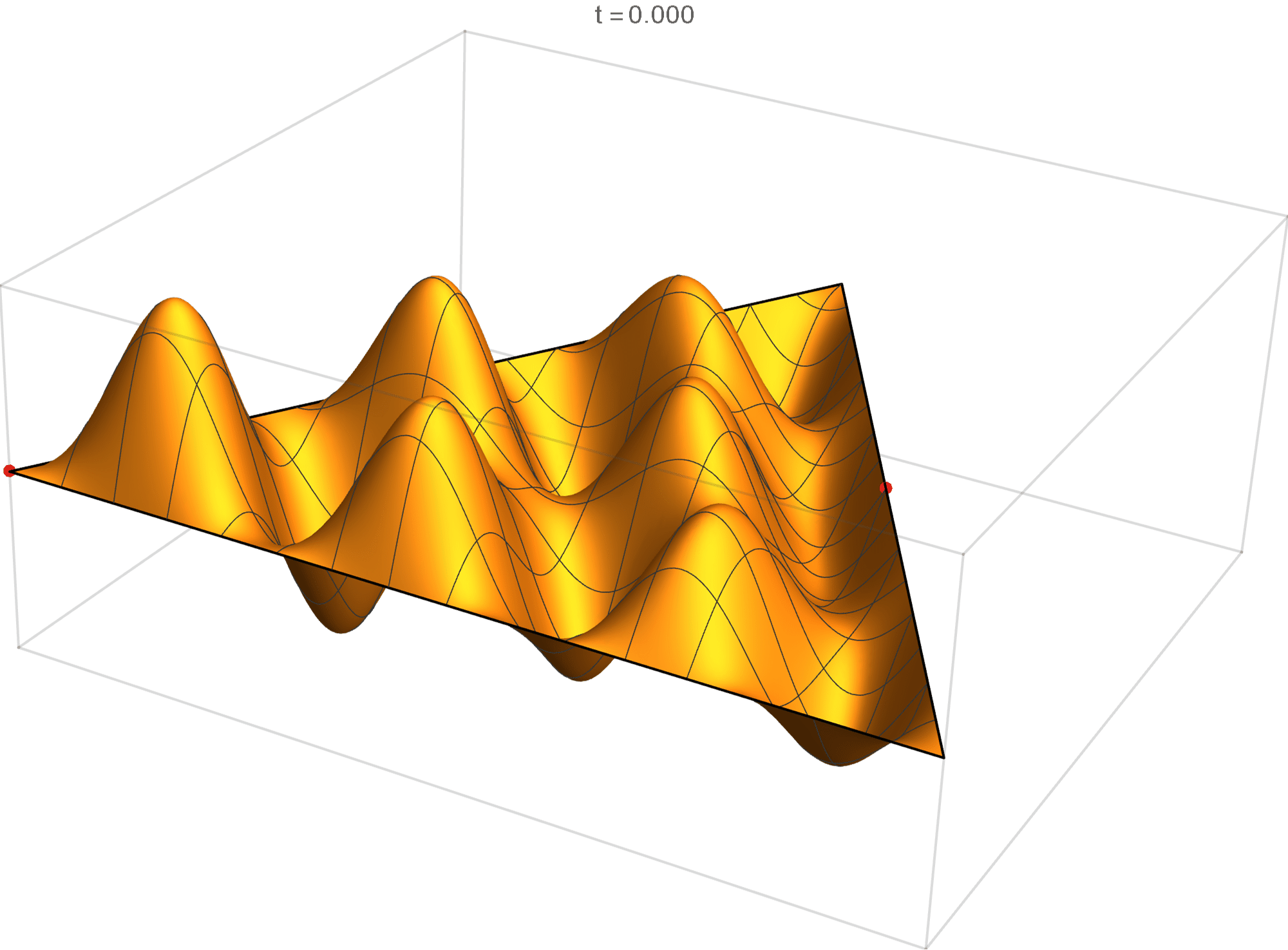
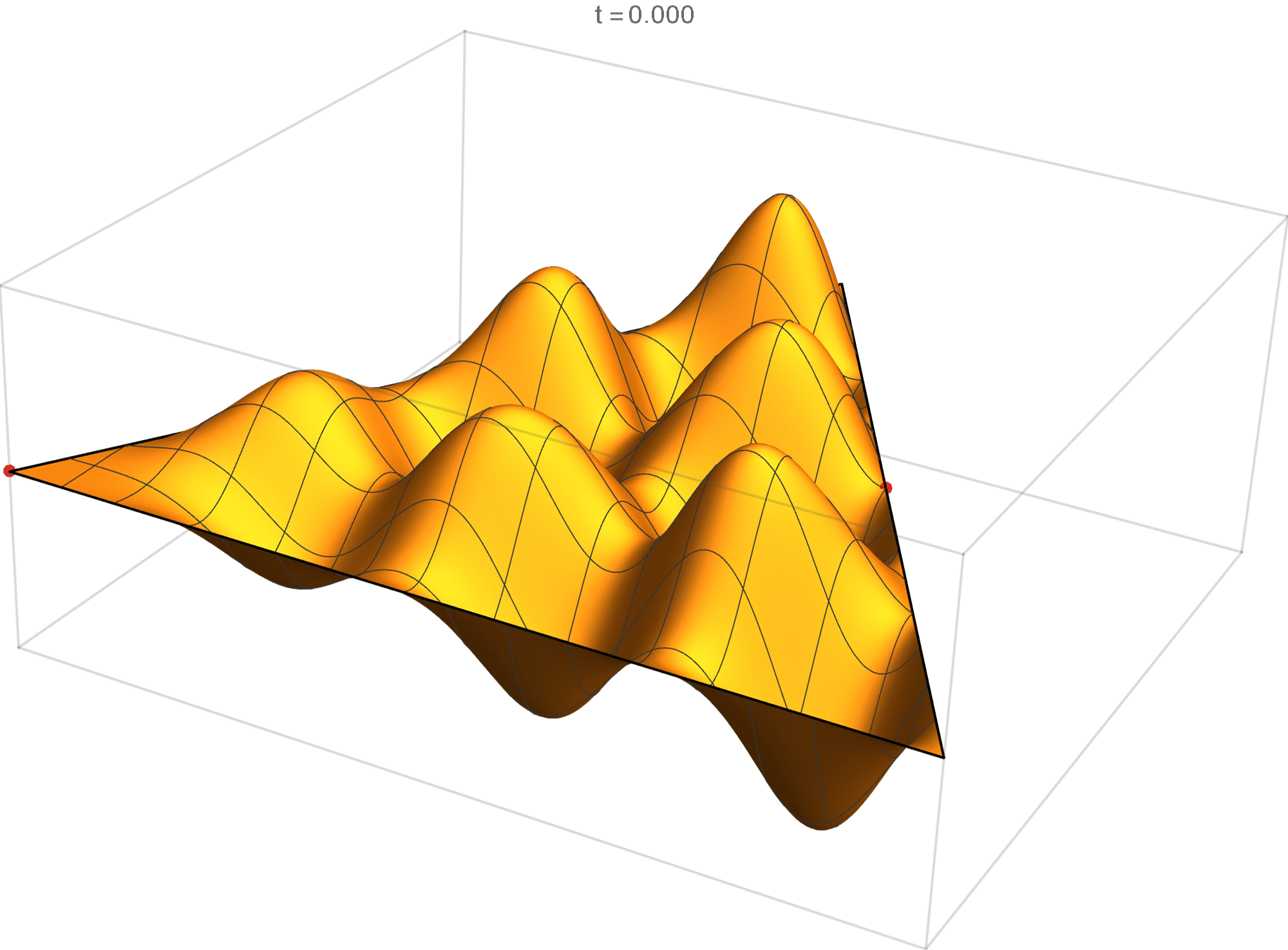
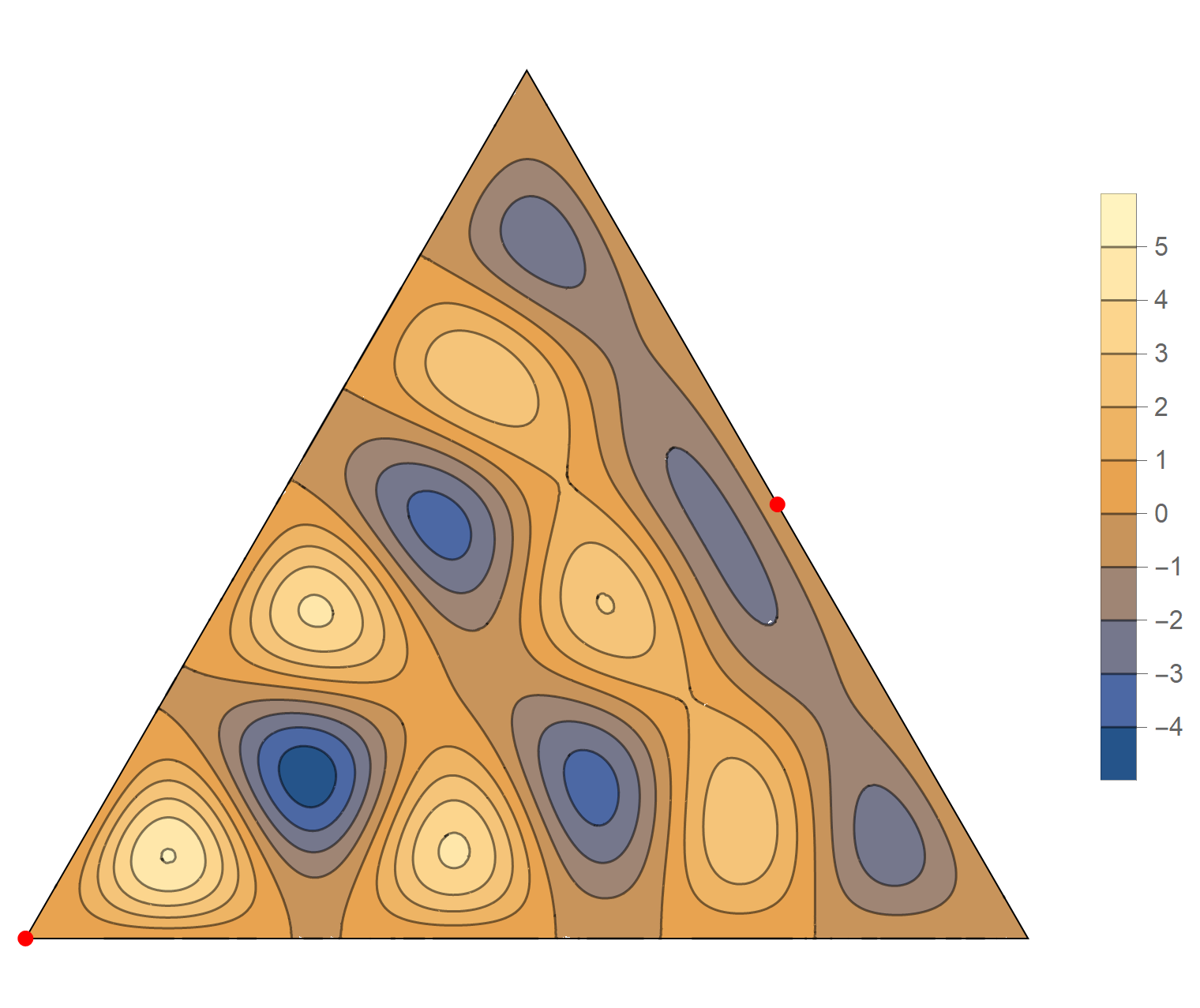
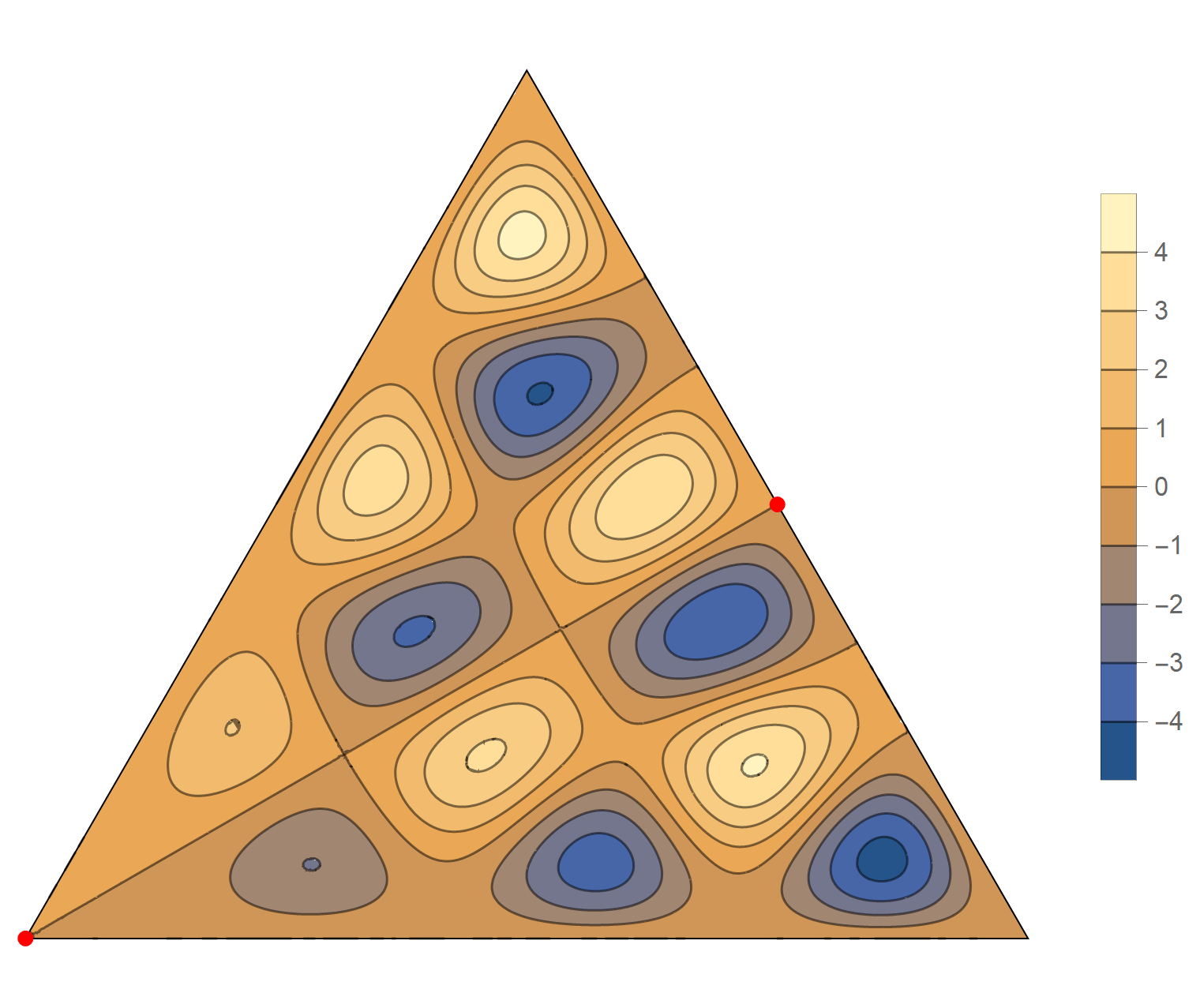
We review the entire two dimensional eigenspace as follows:
\[(\cos\theta)\operatorname{im}(x,y) +(\sin\theta) \operatorname{re}(x,y) \quad \text{as a function of} \quad \theta \in [0,2\pi).\]
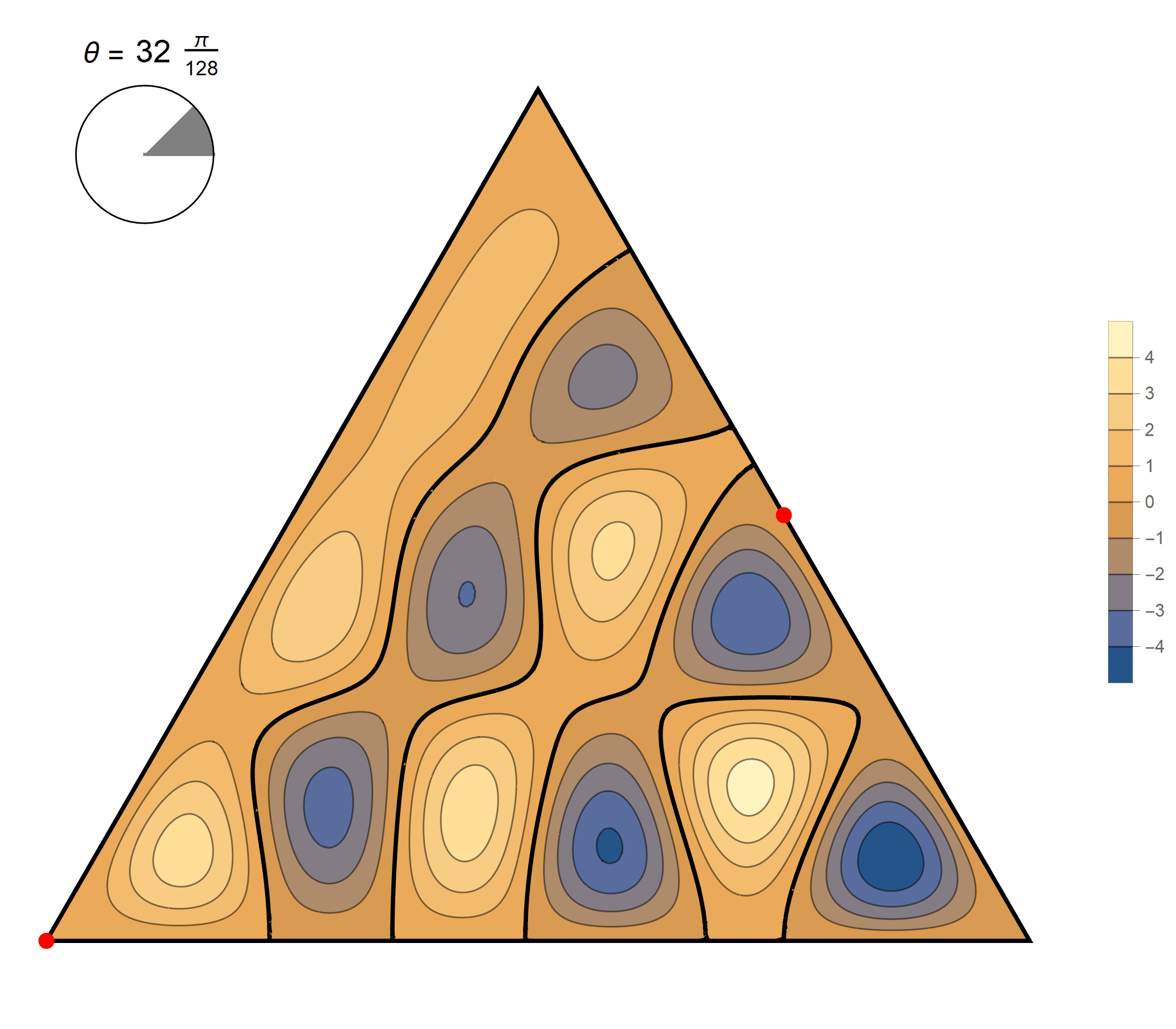
The eleventh eigenvalue has multiplicity 2. The $(m,n)$ pairs that we used to construct the eigenfunction are \[ (9, 12), \quad (9, -3), \quad (-12, -3), \quad (-12, -9), \quad (3, -9), \quad (3, 12). \] The eigenfunctions are
\begin{align*} \operatorname{im}(x,y) & = -\sin \left(\frac{2}{3} \pi \left(3 x-7 \sqrt{3} y\right)\right)+\sin \left(\frac{2}{3} \pi \left(9 x-5 \sqrt{3} y\right)\right)+\sin \left(\frac{2}{3} \pi \left(-12 x-2 \sqrt{3} y\right)\right)\\ &\qquad\qquad -\sin \left(\frac{2}{3} \pi \left(2 \sqrt{3} y-12 x\right)\right)-\sin \left(\frac{2}{3} \pi \left(9 x+5 \sqrt{3} y\right)\right)+\sin \left(\frac{2}{3} \pi \left(3 x+7 \sqrt{3} y\right)\right) \\ \operatorname{re}(x,y) & =-\cos \left(\frac{2}{3} \pi \left(3 x-7 \sqrt{3} y\right)\right)+\cos \left(\frac{2}{3} \pi \left(9 x-5 \sqrt{3} y\right)\right)+\cos \left(\frac{2}{3} \pi \left(-12 x-2 \sqrt{3} y\right)\right)\\ &\qquad\qquad -\cos \left(\frac{2}{3} \pi \left(2 \sqrt{3} y-12 x\right)\right)-\cos \left(\frac{2}{3} \pi \left(9 x+5 \sqrt{3} y\right)\right)+\cos \left(\frac{2}{3} \pi \left(3 x+7 \sqrt{3} y\right)\right) \end{align*}
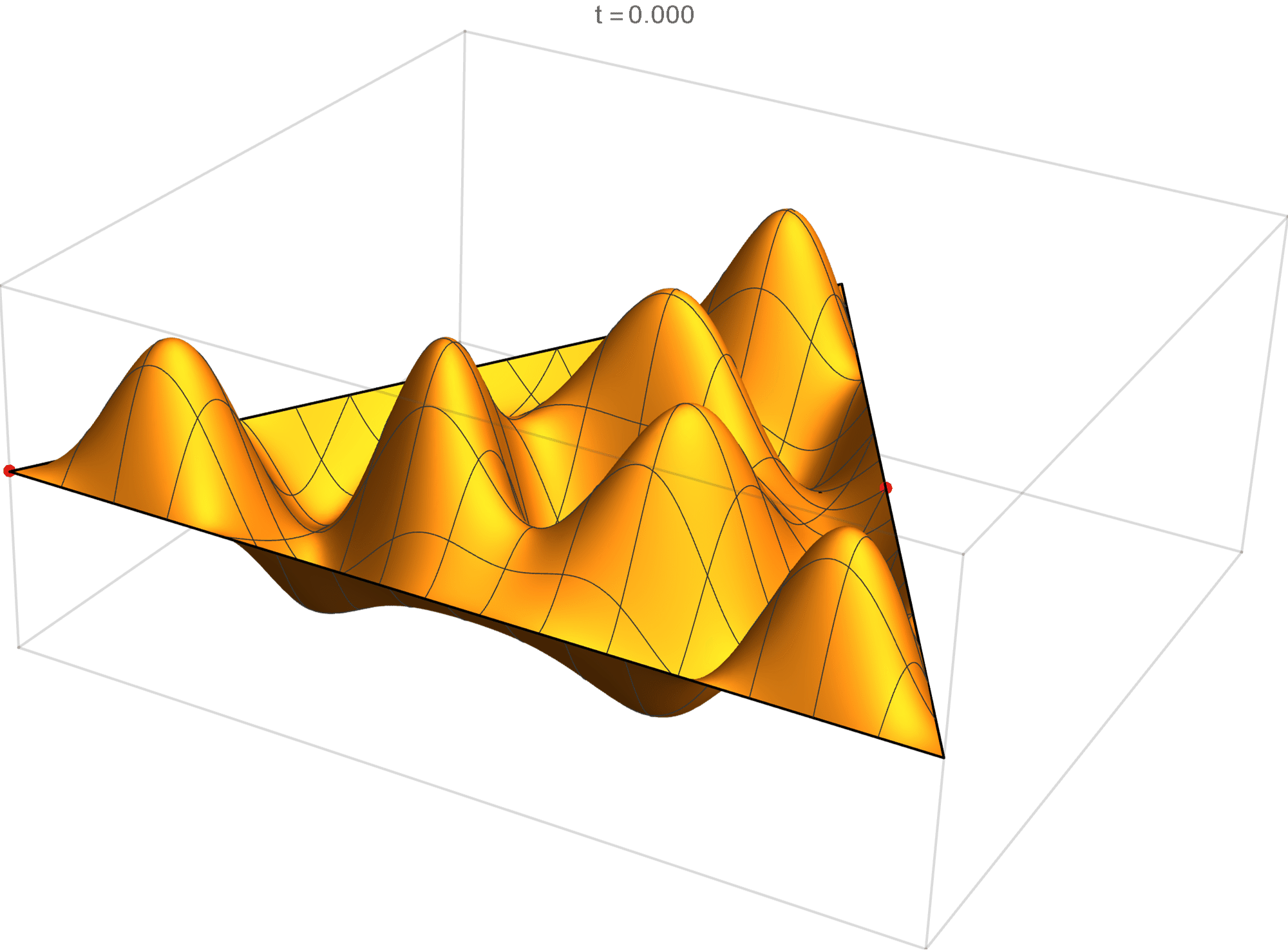
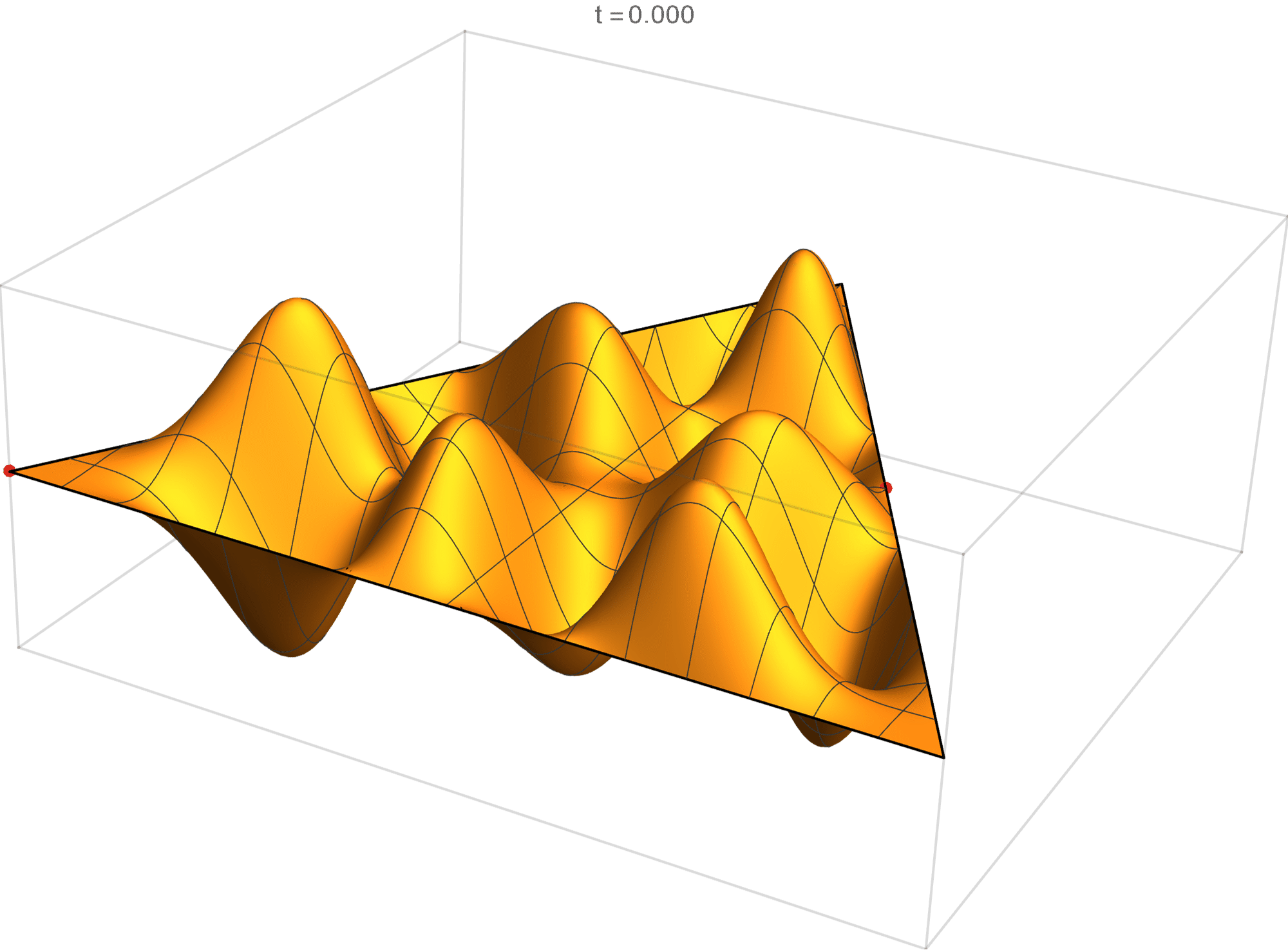
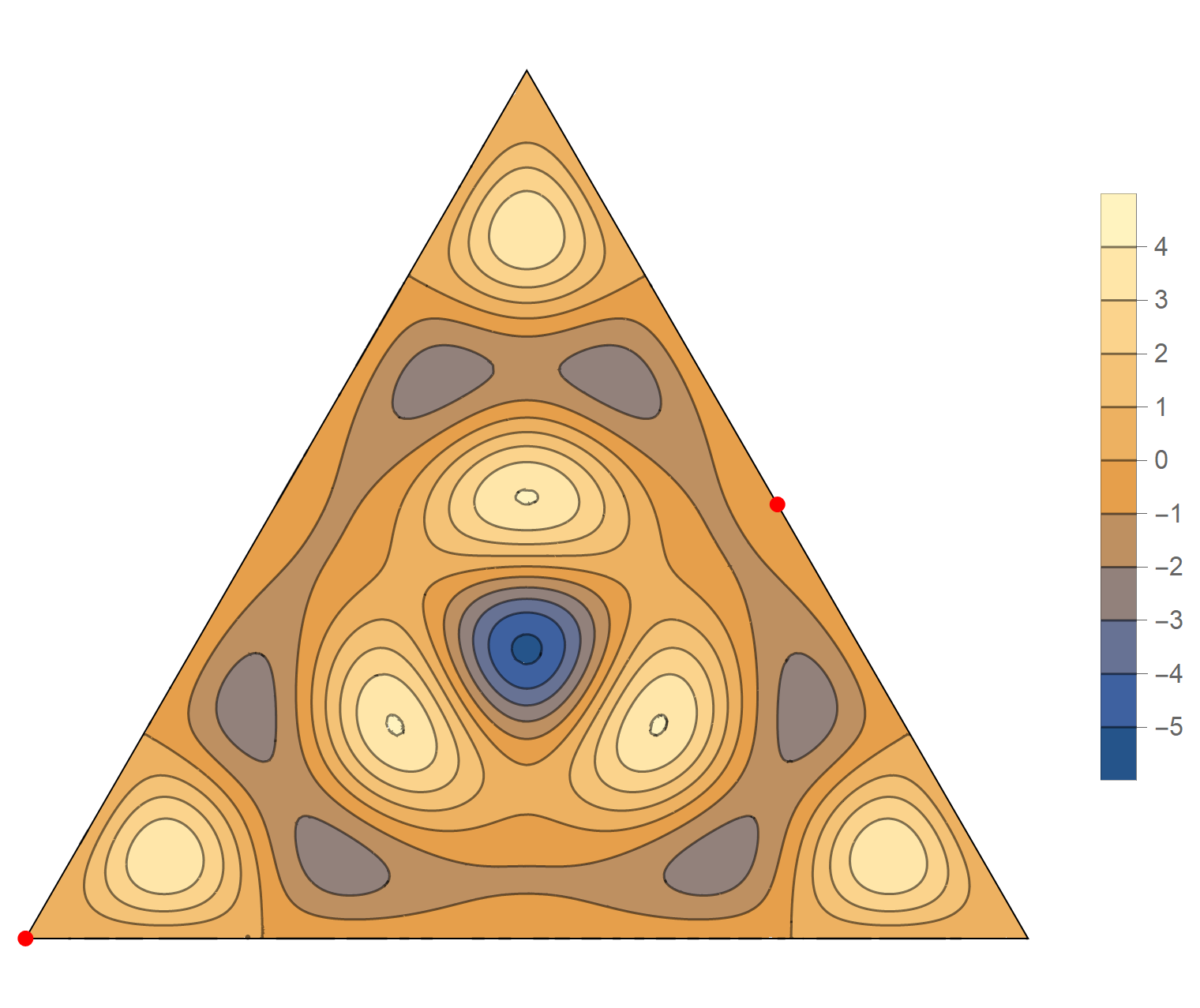
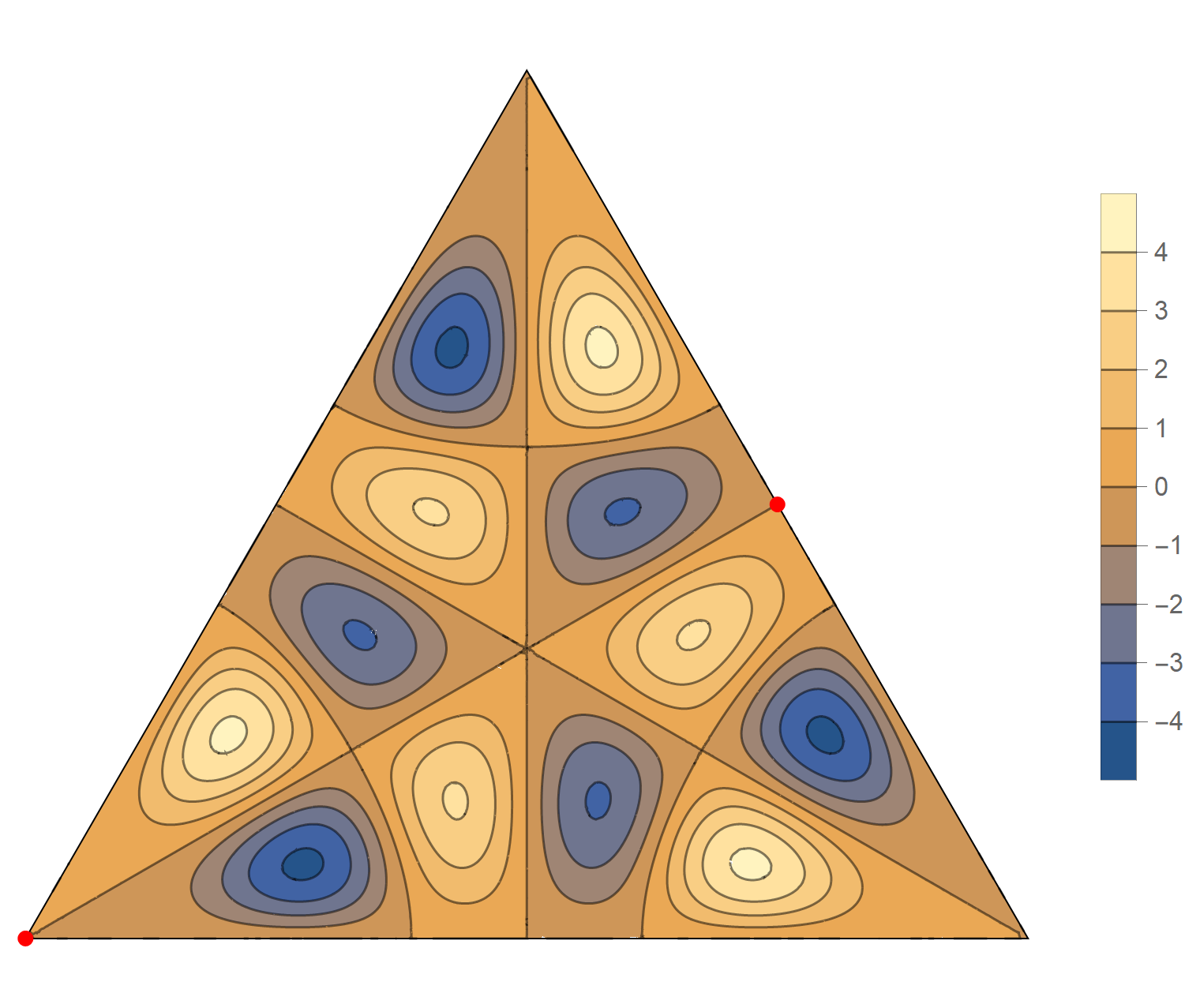
We review the entire two dimensional eigenspace as follows:
\[(\cos\theta)\operatorname{im}(x,y) +(\sin\theta) \operatorname{re}(x,y) \quad \text{as a function of} \quad \theta \in [0,2\pi).\]
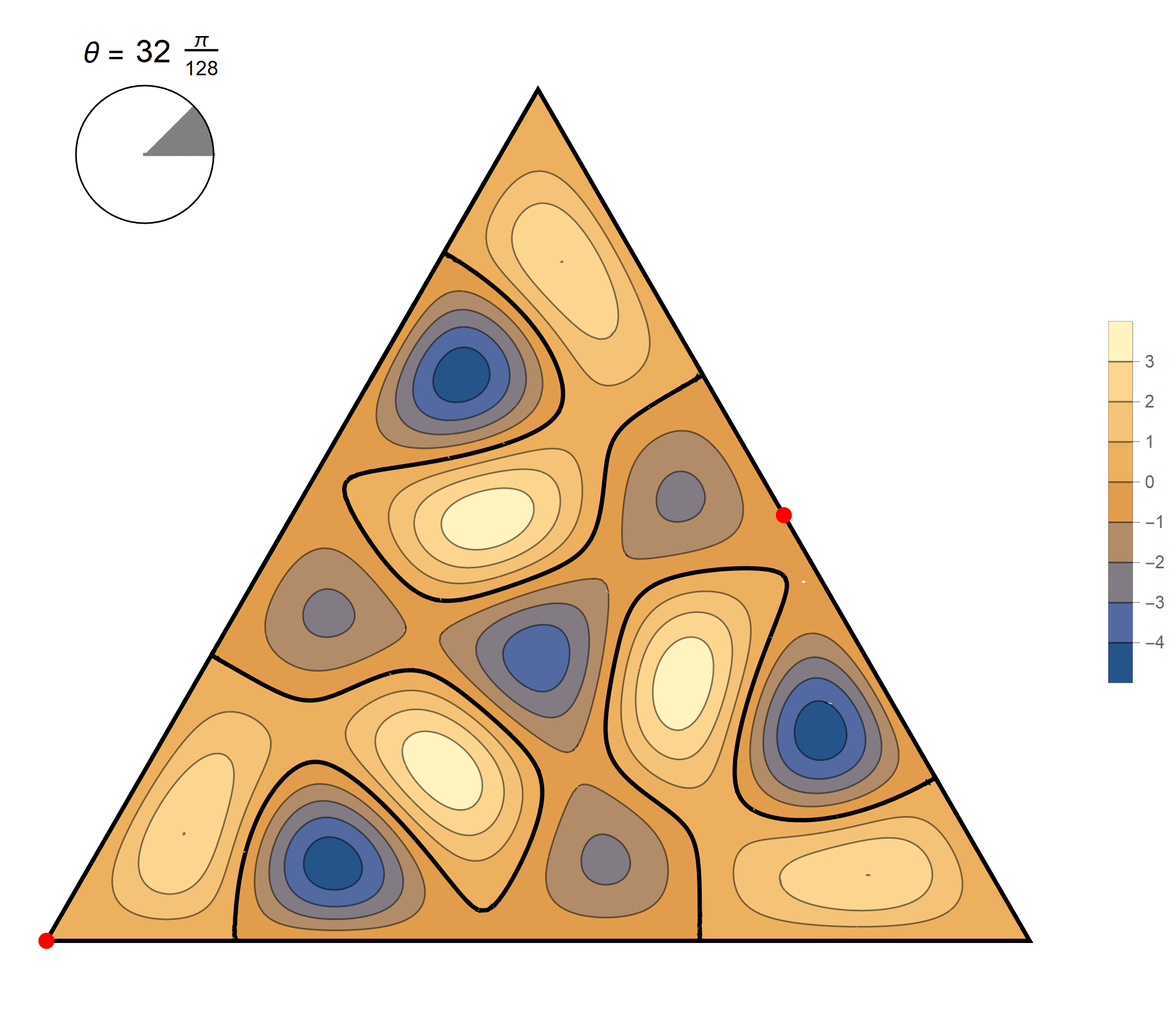
The twelfth eigenvalue has multiplicity 2. The $(m,n)$ pairs that we used to construct the eigenfunction are \[ (8, 13), \quad (8, -5), \quad (-13, -5), \quad (-13, -8), \quad (5, -8), \quad (5, 13). \] The eigenfunctions are
\begin{align*} \operatorname{im}(x,y) & =-\sin \left(\frac{2}{3} \pi \left(5 x-7 \sqrt{3} y\right)\right)+\sin \left(\frac{2}{3} \pi \left(8 x-6 \sqrt{3} y\right)\right)+\sin \left(\frac{2}{3} \pi \left(-13 x-\sqrt{3} y\right)\right)\\ &\qquad\qquad-\sin \left(\frac{2}{3} \pi \left(\sqrt{3} y-13 x\right)\right)-\sin \left(\frac{2}{3} \pi \left(8 x+6 \sqrt{3} y\right)\right)+\sin \left(\frac{2}{3} \pi \left(5 x+7 \sqrt{3} y\right)\right) \\ \operatorname{re}(x,y) & = -\cos \left(\frac{2}{3} \pi \left(5 x-7 \sqrt{3} y\right)\right)+\cos \left(\frac{2}{3} \pi \left(8 x-6 \sqrt{3} y\right)\right)+\cos \left(\frac{2}{3} \pi \left(-13 x-\sqrt{3} y\right)\right)\\ &\qquad\qquad-\cos \left(\frac{2}{3} \pi \left(\sqrt{3} y-13 x\right)\right)-\cos \left(\frac{2}{3} \pi \left(8 x+6 \sqrt{3} y\right)\right)+\cos \left(\frac{2}{3} \pi \left(5 x+7 \sqrt{3} y\right)\right) \end{align*}
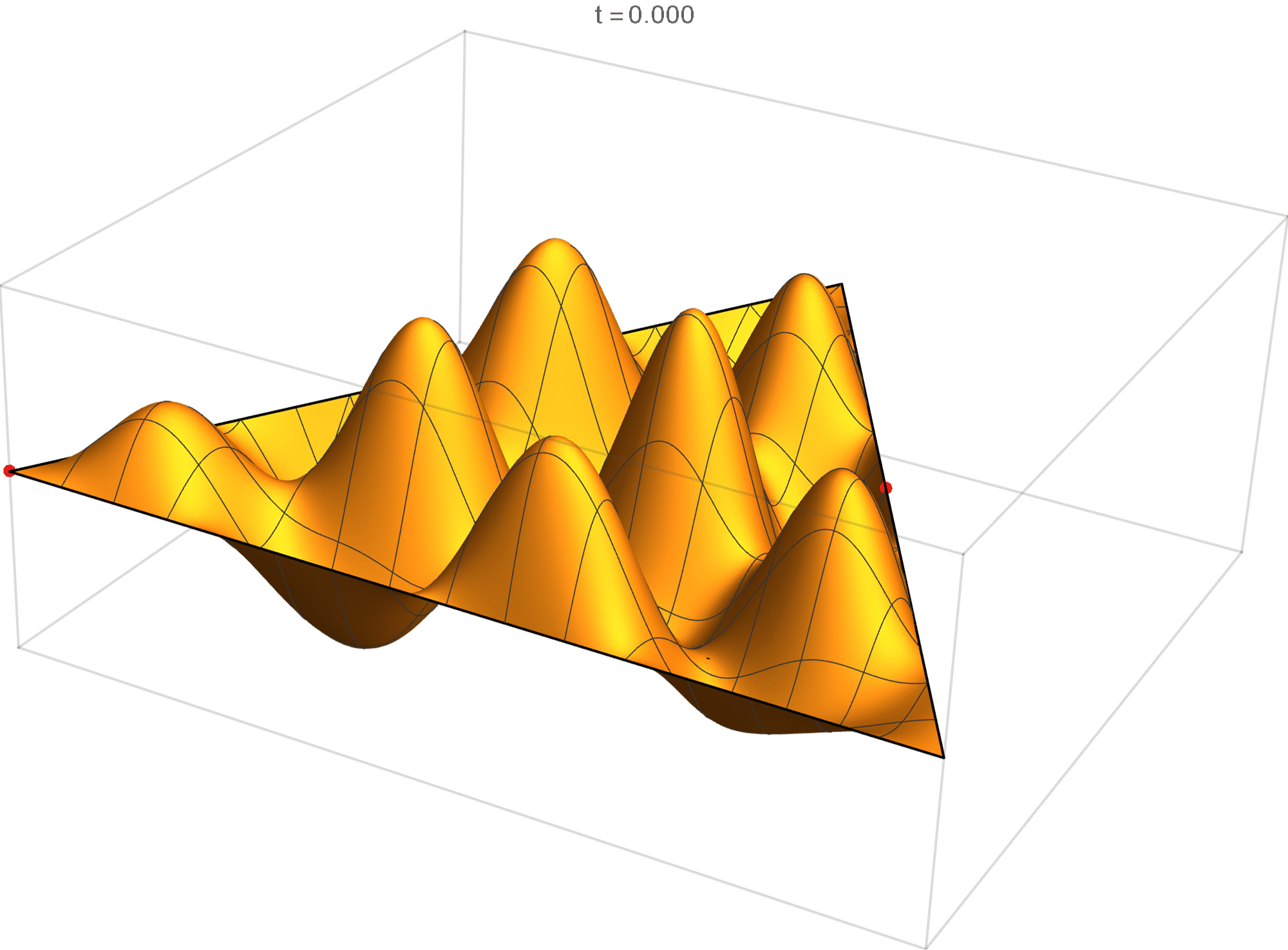
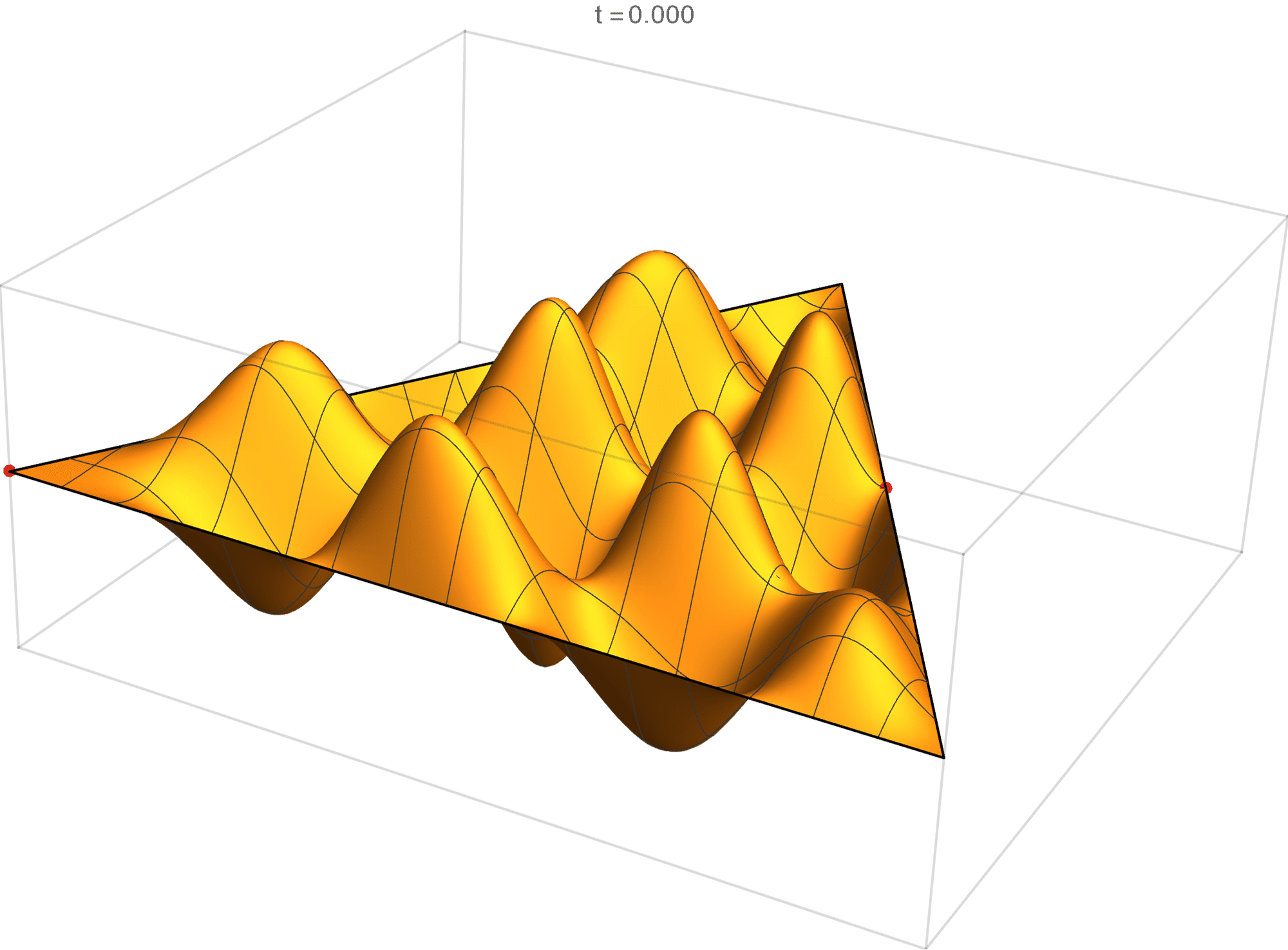
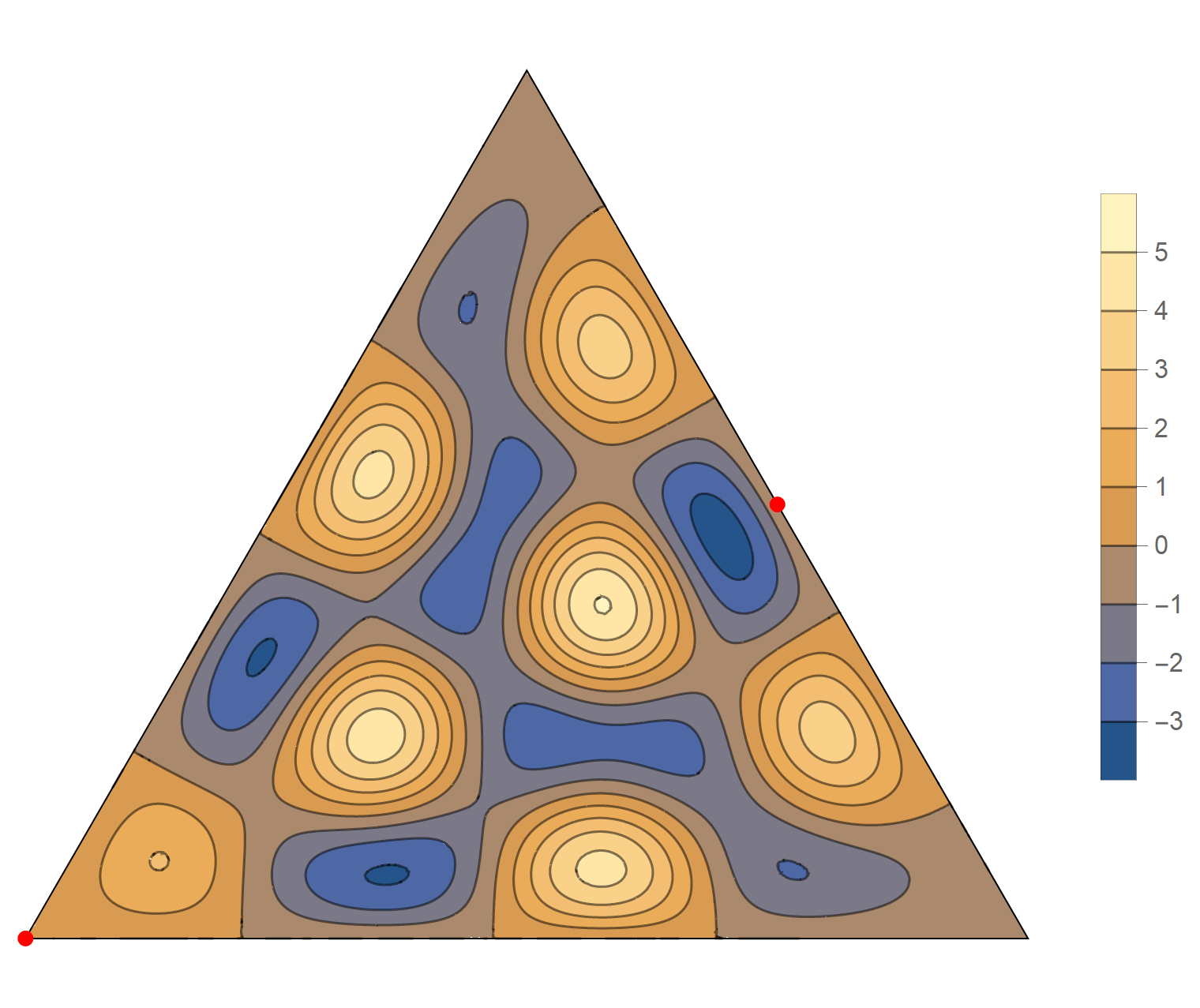
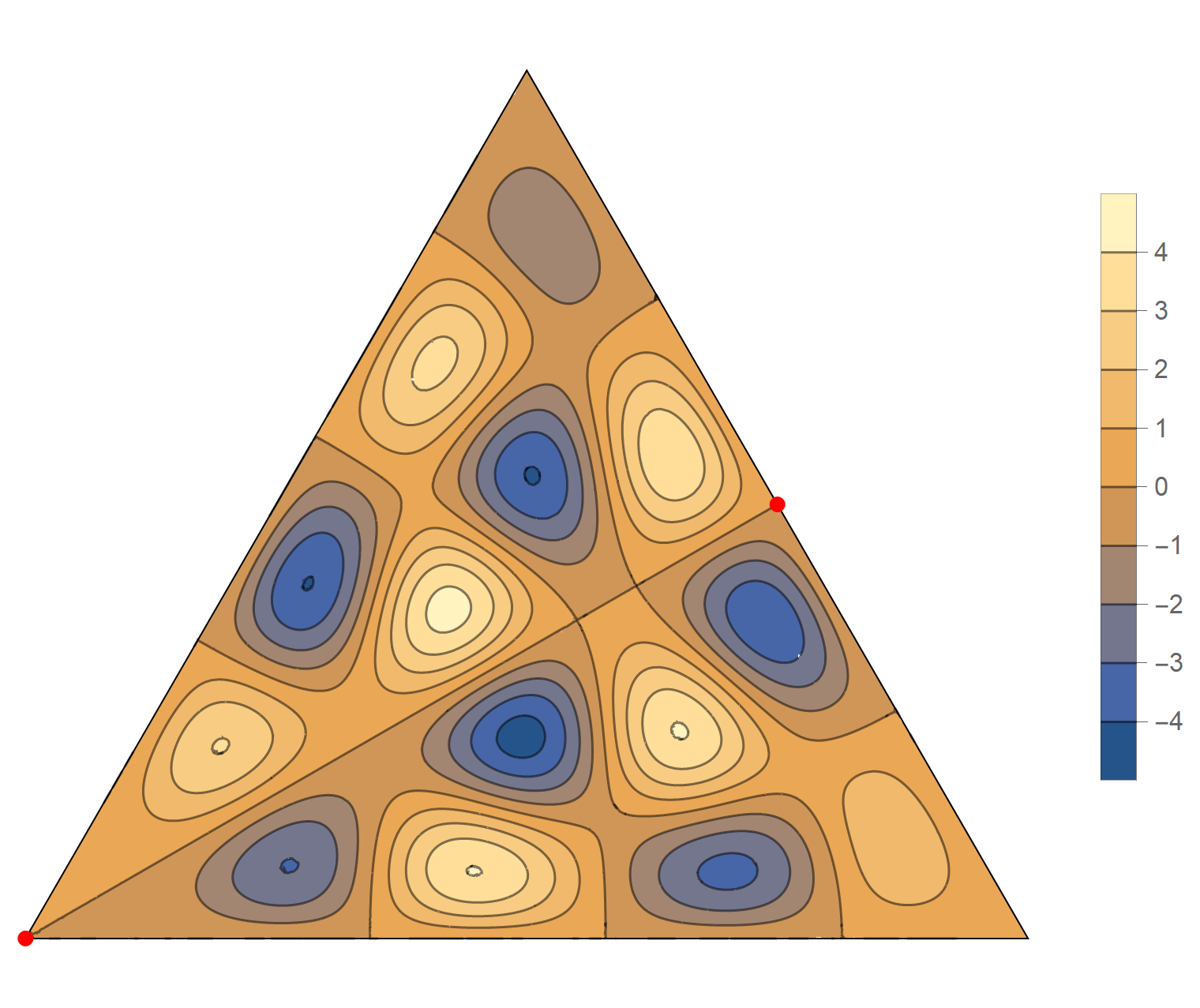
We review the entire two dimensional eigenspace as follows:
\[(\cos\theta)\operatorname{im}(x,y) +(\sin\theta) \operatorname{re}(x,y) \quad \text{as a function of} \quad \theta \in [0,2\pi).\]
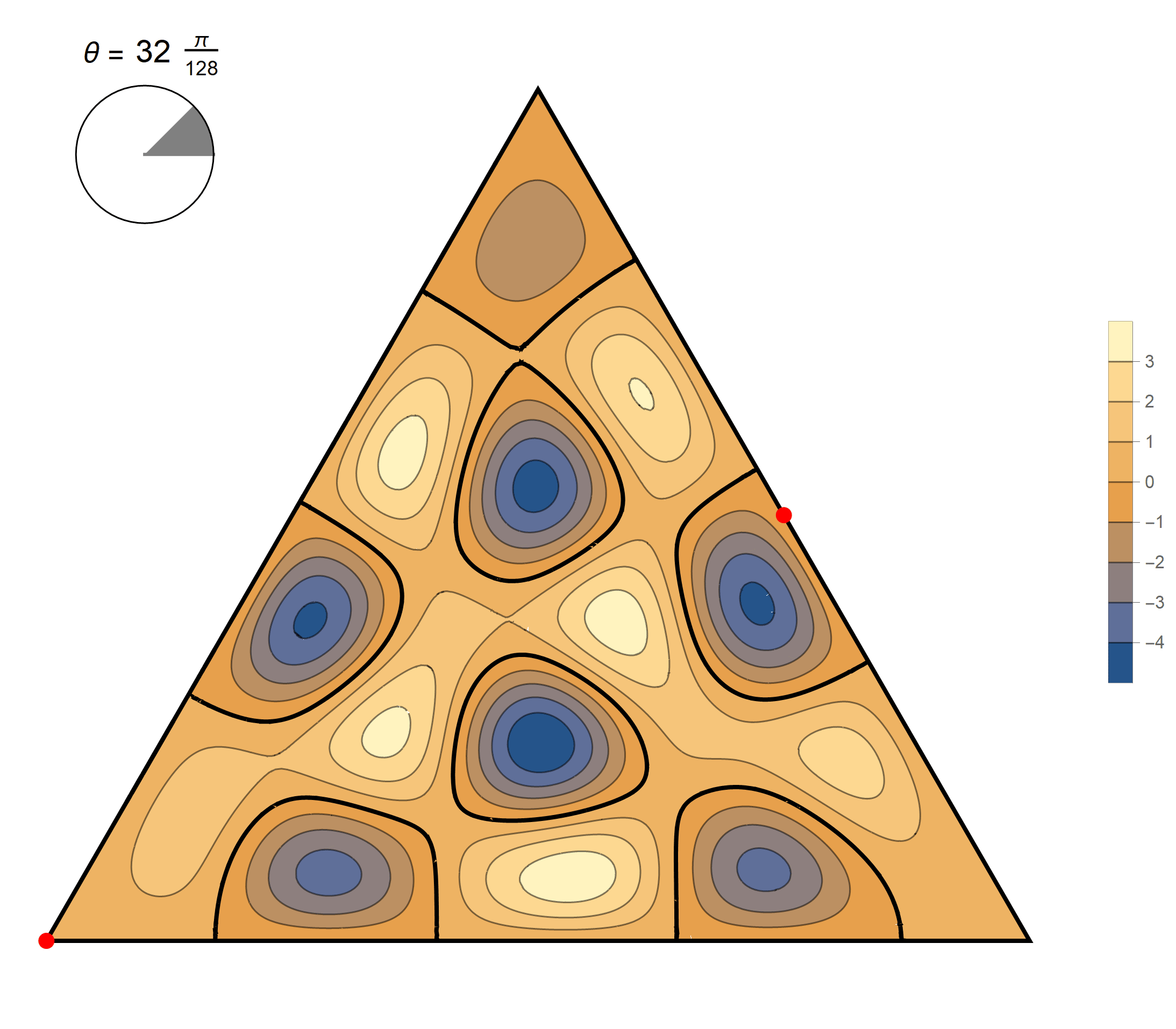
The thirteenth eigenvalue is simple. The $(m,n)$ pairs that we used to construct the eigenfunction are \[ (12, 12), \quad (12, 0), \quad (-12,0), \quad (-12, -12), \quad (0,-12), \quad (0,12). \] The eigenfunctions are
\[ \operatorname{im}(x,y) =2 \sin \left(\frac{2}{3} \pi \left(12 x-4 \sqrt{3} y\right)\right) -2 \sin \left(\frac{2}{3} \pi \left(12x+4 \sqrt{3} y\right)\right) +2 \sin \left(\frac{16 \pi y}{\sqrt{3}}\right) \]
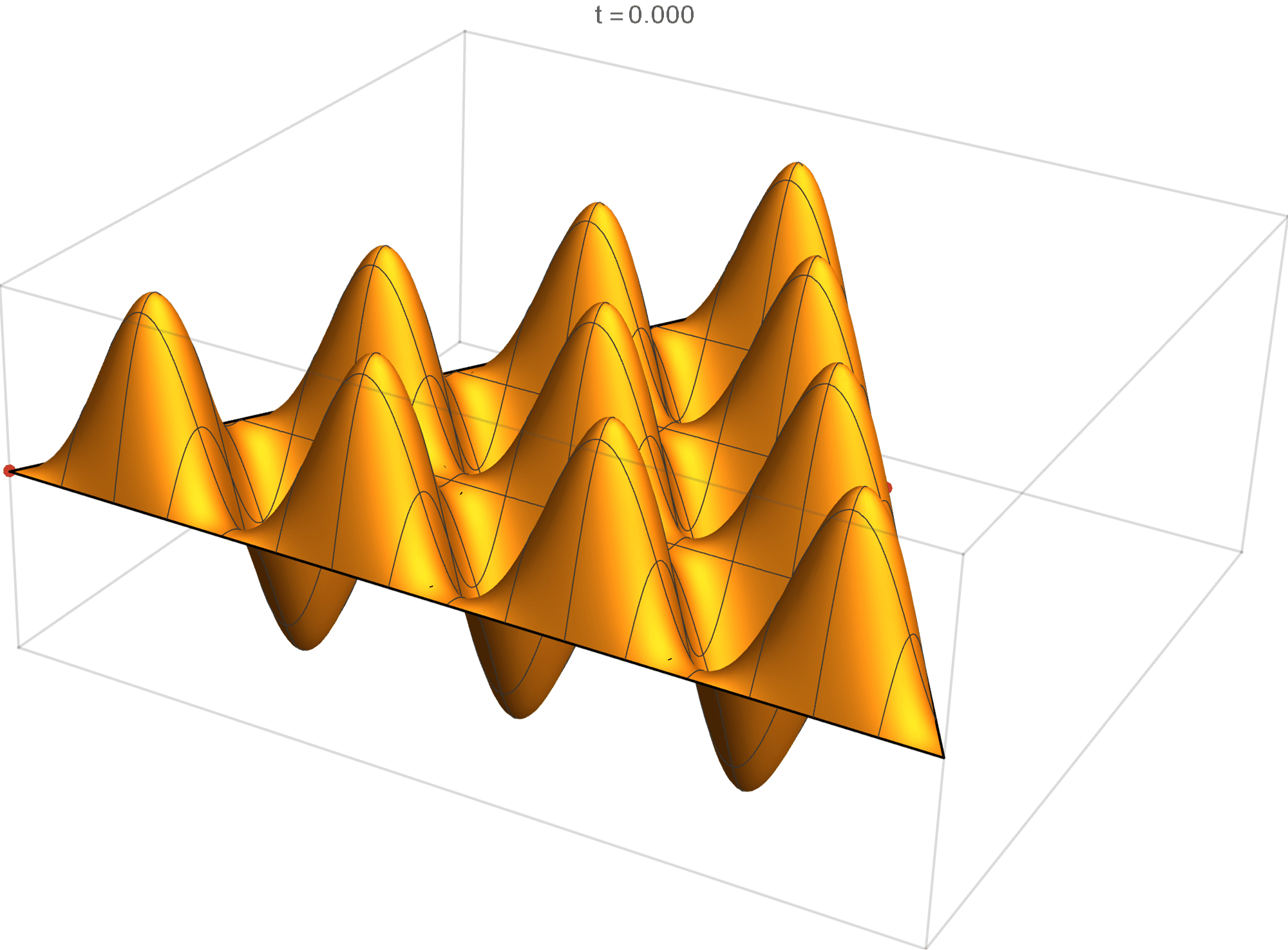
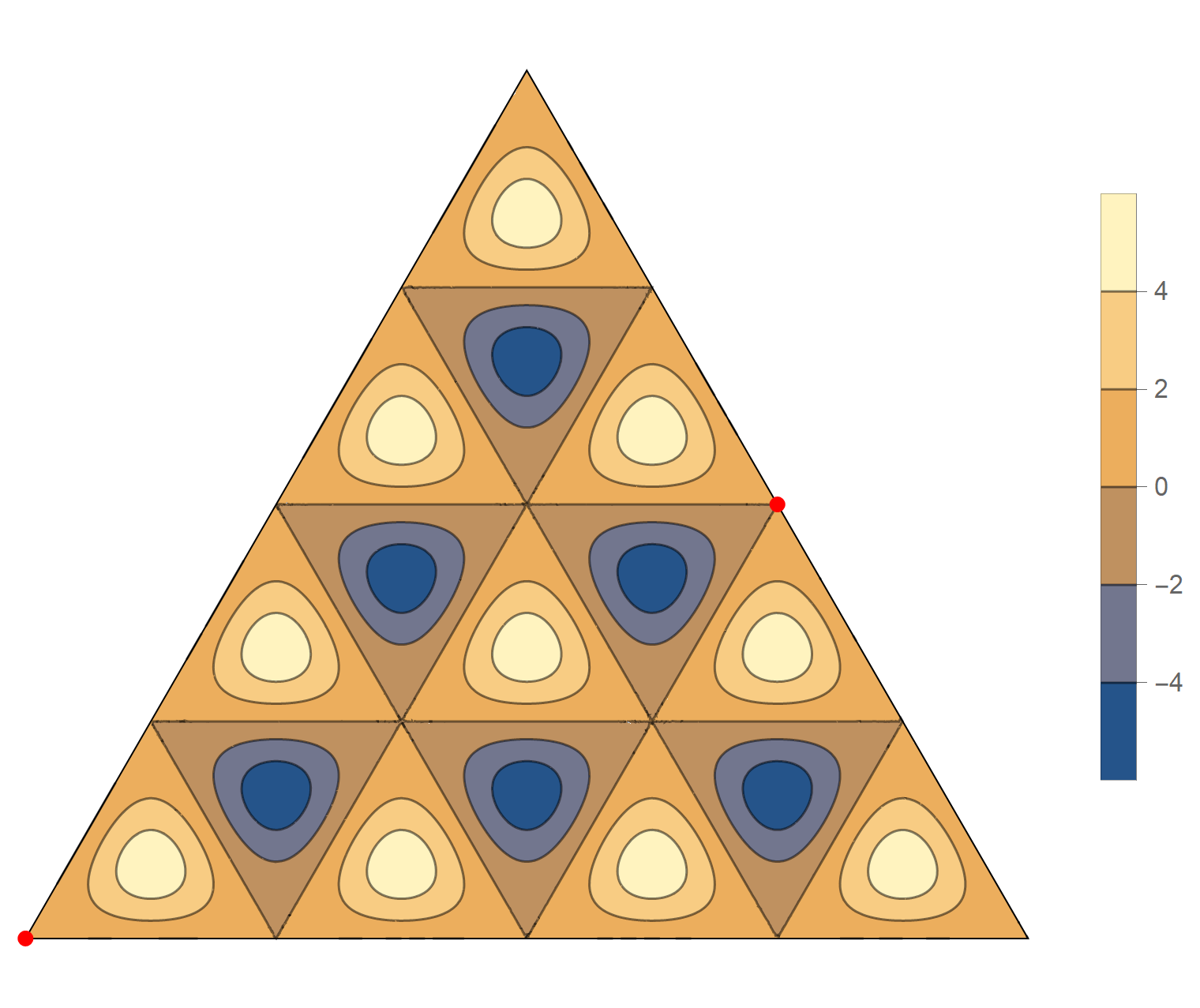
The fourteenth eigenvalue has multiplicity 2. The $(m,n)$ pairs that we used to construct the eigenfunction are \[ (11, 13), \quad (11, -2), \quad (-13, -2), \quad (-13, -11), \quad (2, -11), \quad (2, 13). \] The eigenfunctions are
\begin{align*} \operatorname{im}(x,y) & = -\sin \left(\frac{2}{3} \pi \left(2 x-8 \sqrt{3} y\right)\right)+\sin \left(\frac{2}{3} \pi \left(11 x-5 \sqrt{3} y\right)\right)+\sin \left(\frac{2}{3} \pi \left(-13 x-3 \sqrt{3} y\right)\right)\\ &\qquad\qquad-\sin \left(\frac{2}{3} \pi \left(3 \sqrt{3} y-13 x\right)\right)-\sin \left(\frac{2}{3} \pi \left(11 x+5 \sqrt{3} y\right)\right)+\sin \left(\frac{2}{3} \pi \left(2 x+8 \sqrt{3} y\right)\right) \\ \operatorname{re}(x,y) & =-\cos \left(\frac{2}{3} \pi \left(2 x-8 \sqrt{3} y\right)\right)+\cos \left(\frac{2}{3} \pi \left(11 x-5 \sqrt{3} y\right)\right)+\cos \left(\frac{2}{3} \pi \left(-13 x-3 \sqrt{3} y\right)\right)\\ &\qquad\qquad-\cos \left(\frac{2}{3} \pi \left(3 \sqrt{3} y-13 x\right)\right)-\cos \left(\frac{2}{3} \pi \left(11 x+5 \sqrt{3} y\right)\right)+\cos \left(\frac{2}{3} \pi \left(2 x+8 \sqrt{3} y\right)\right) \end{align*}
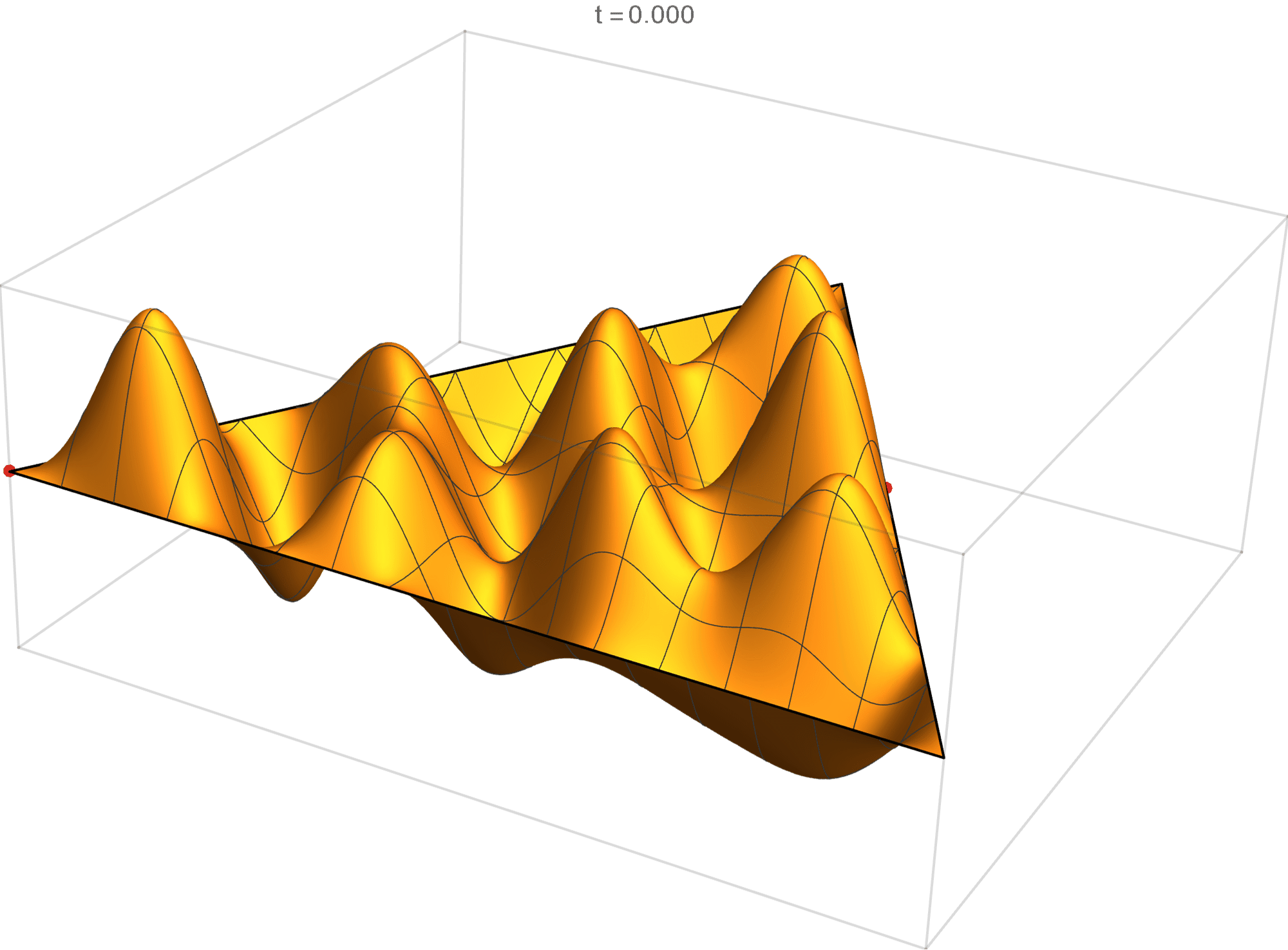
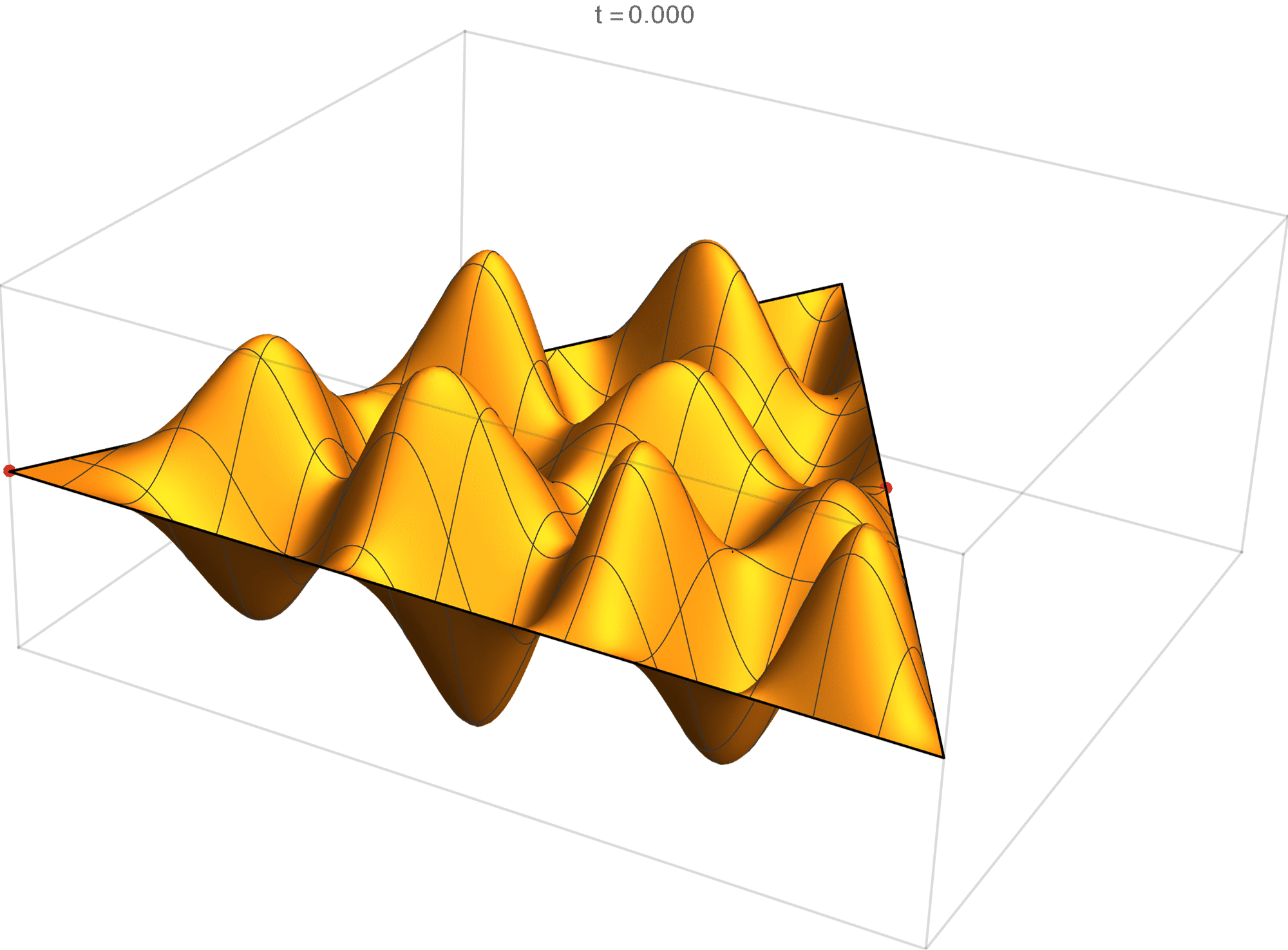
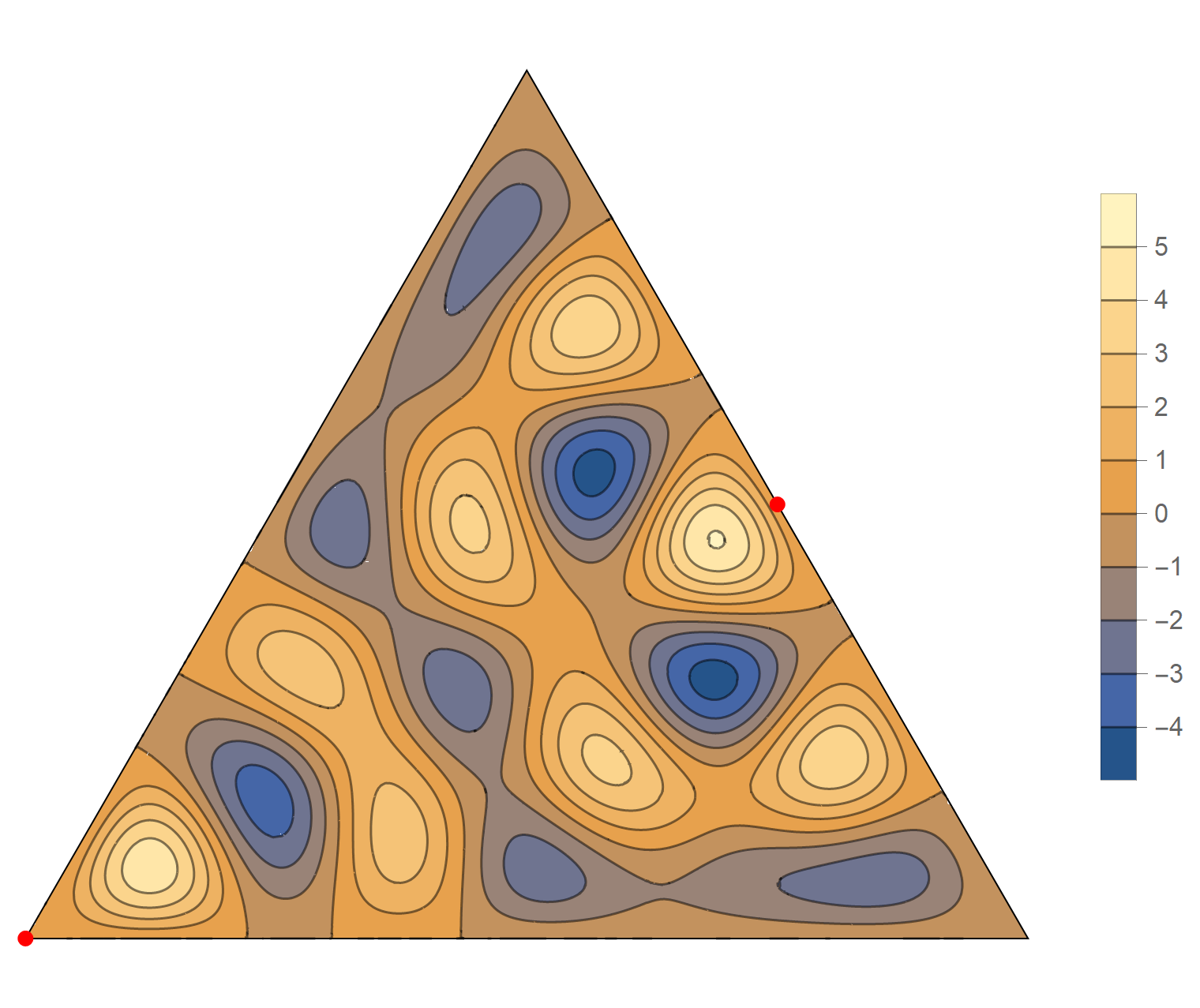
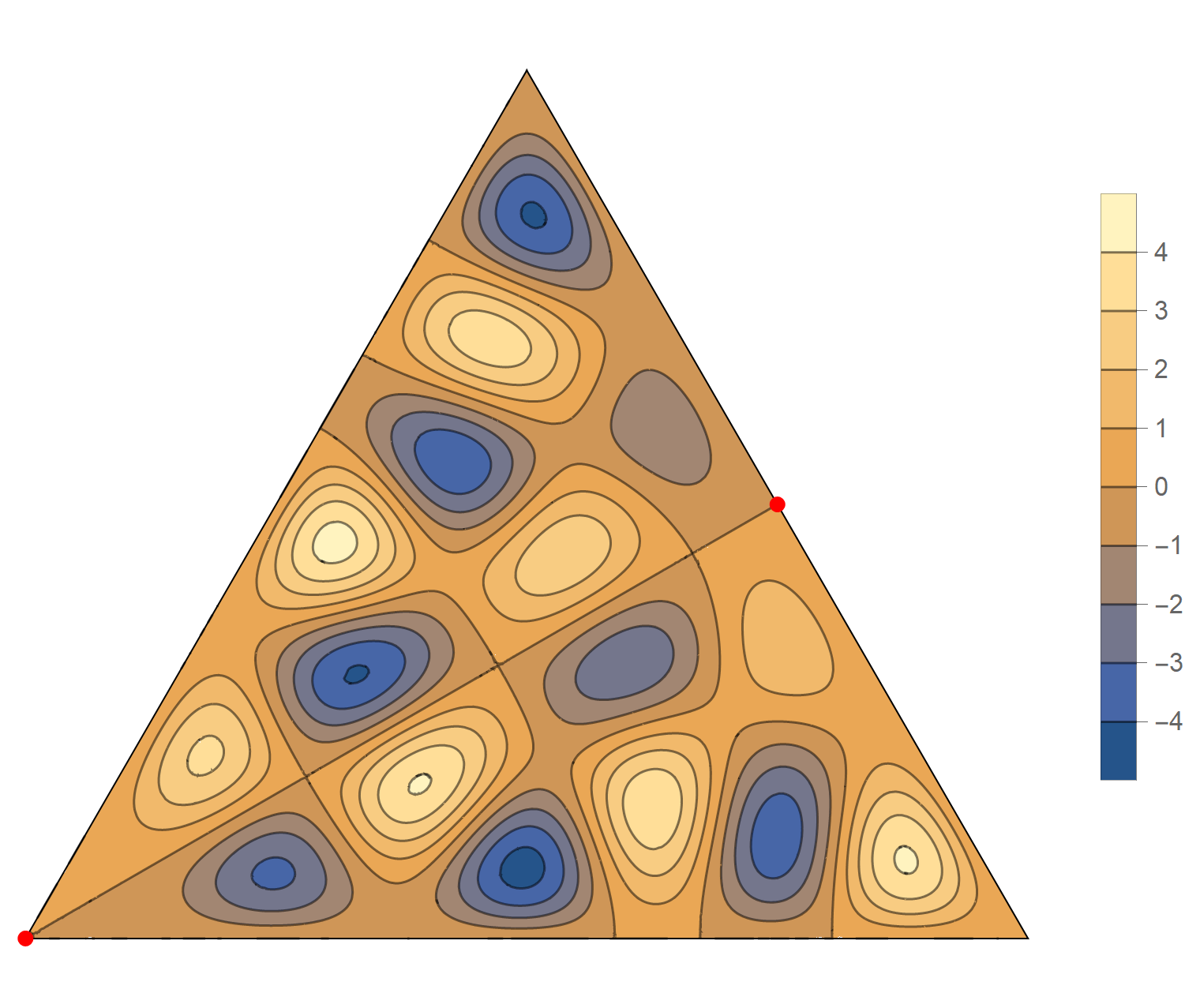
We review the entire two dimensional eigenspace as follows:
\[(\cos\theta)\operatorname{im}(x,y) +(\sin\theta) \operatorname{re}(x,y) \quad \text{as a function of} \quad \theta \in [0,2\pi).\]
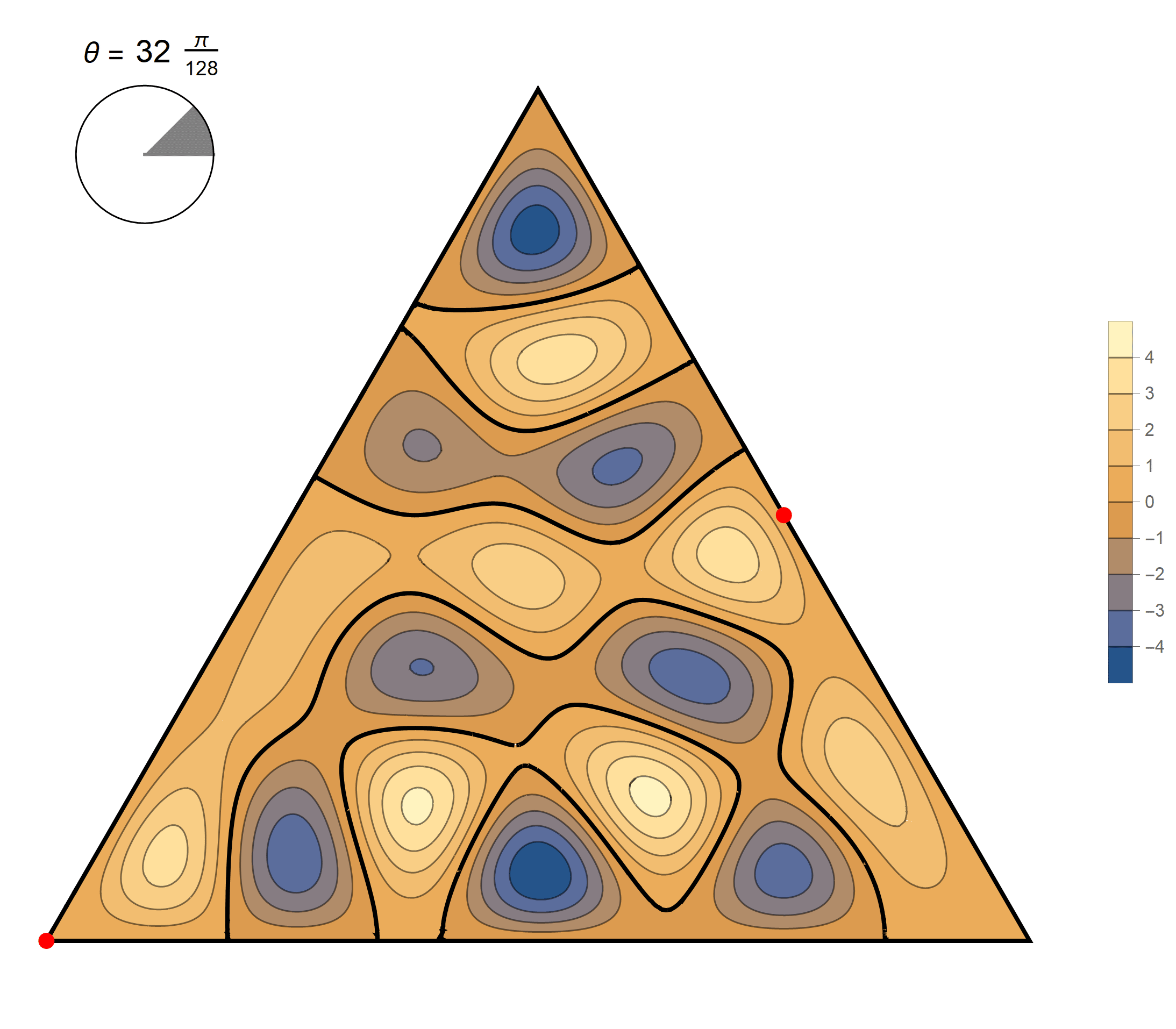
The fifteenth eigenvalue has multiplicity 2. The $(m,n)$ pairs that we used to construct the eigenfunction are \[ (10, 14), \quad (10, -4), \quad (-14, -4), \quad (-14, -10), \quad (4, -10), \quad (4, 14). \] The eigenfunctions are
\begin{align*} \operatorname{im}(x,y) & = -\sin \left(\frac{2}{3} \pi \left(4 x-8 \sqrt{3} y\right)\right)+\sin \left(\frac{2}{3} \pi \left(10 x-6 \sqrt{3} y\right)\right)+\sin \left(\frac{2}{3} \pi \left(-14 x-2 \sqrt{3} y\right)\right)\\ &\qquad\qquad-\sin \left(\frac{2}{3} \pi \left(2 \sqrt{3} y-14 x\right)\right)-\sin \left(\frac{2}{3} \pi \left(10 x+6 \sqrt{3} y\right)\right)+\sin \left(\frac{2}{3} \pi \left(4 x+8 \sqrt{3} y\right)\right) \\ \operatorname{re}(x,y) & =-\cos \left(\frac{2}{3} \pi \left(4 x-8 \sqrt{3} y\right)\right)+\cos \left(\frac{2}{3} \pi \left(10 x-6 \sqrt{3} y\right)\right)+\cos \left(\frac{2}{3} \pi \left(-14 x-2 \sqrt{3} y\right)\right)\\ &\qquad\qquad-\cos \left(\frac{2}{3} \pi \left(2 \sqrt{3} y-14 x\right)\right)-\cos \left(\frac{2}{3} \pi \left(10 x+6 \sqrt{3} y\right)\right)+\cos \left(\frac{2}{3} \pi \left(4 x+8 \sqrt{3} y\right)\right) \end{align*}
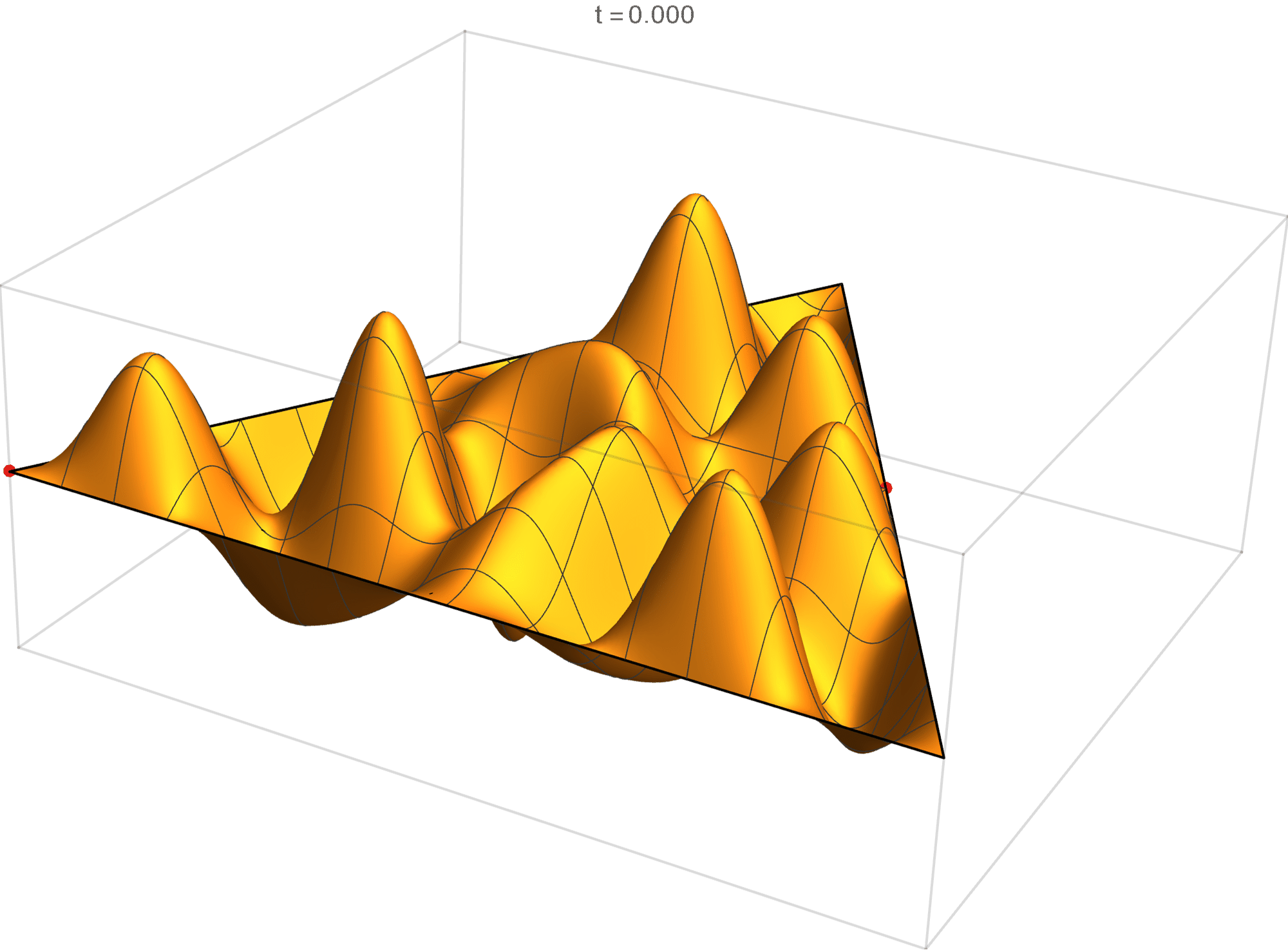
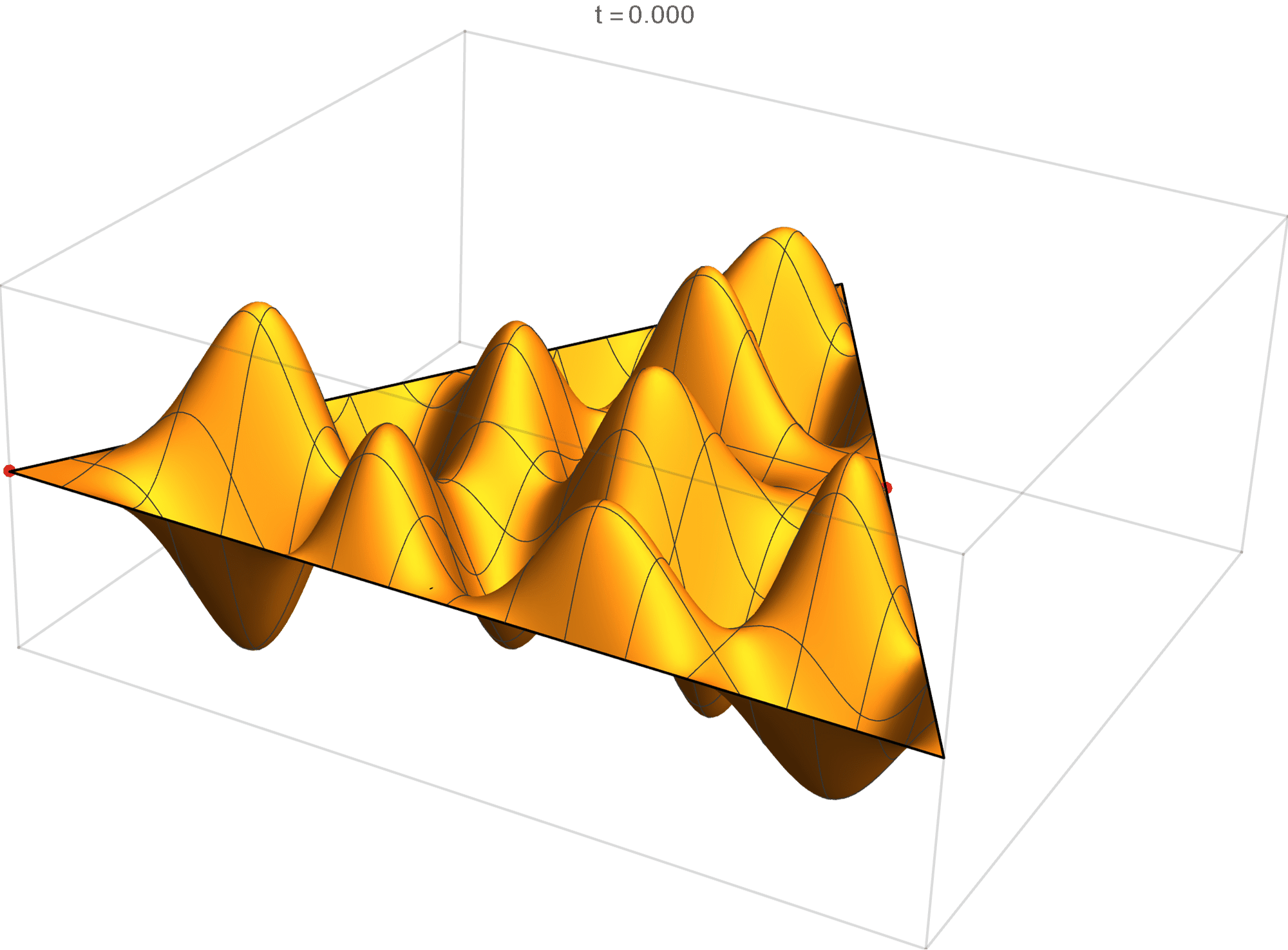
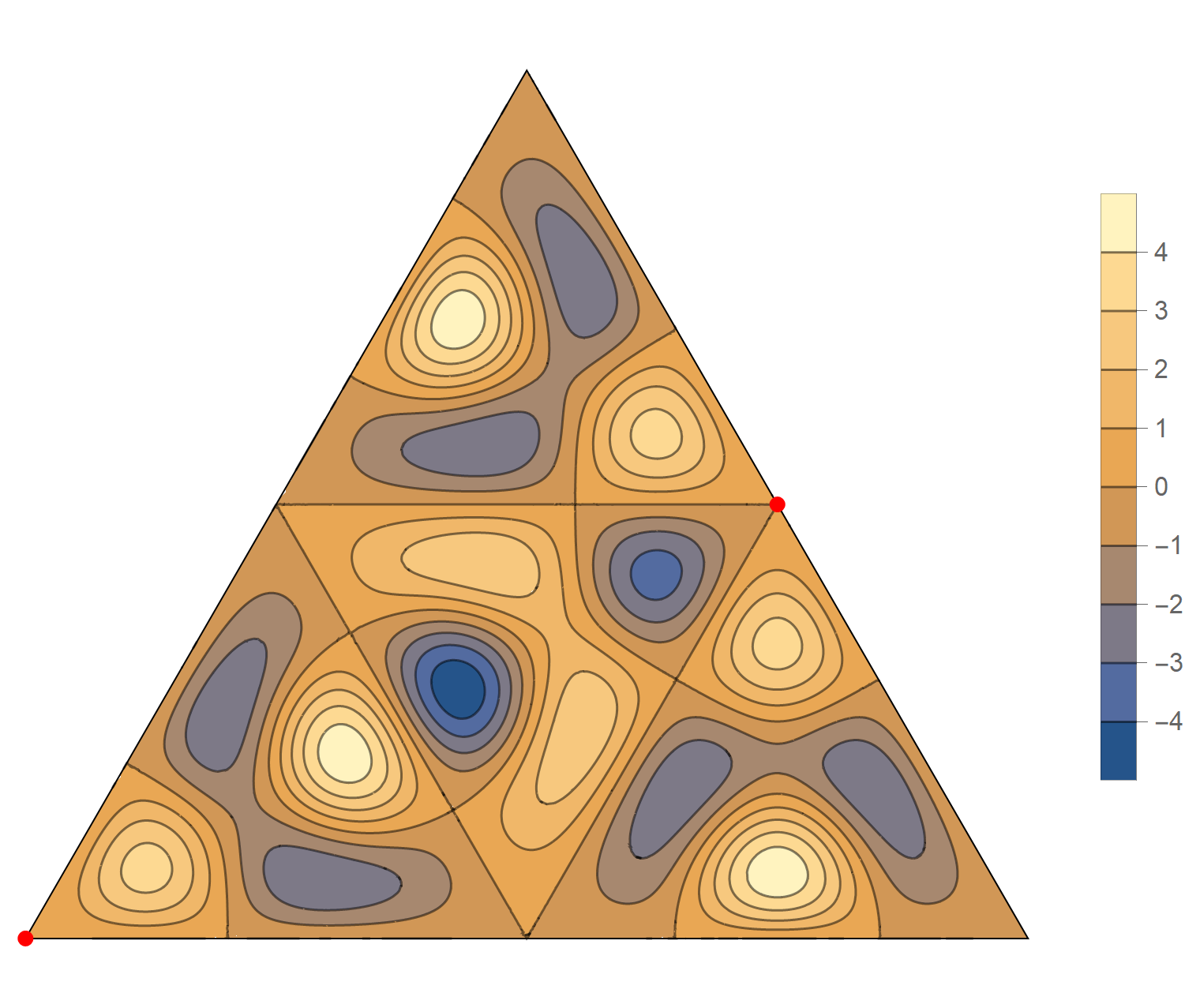
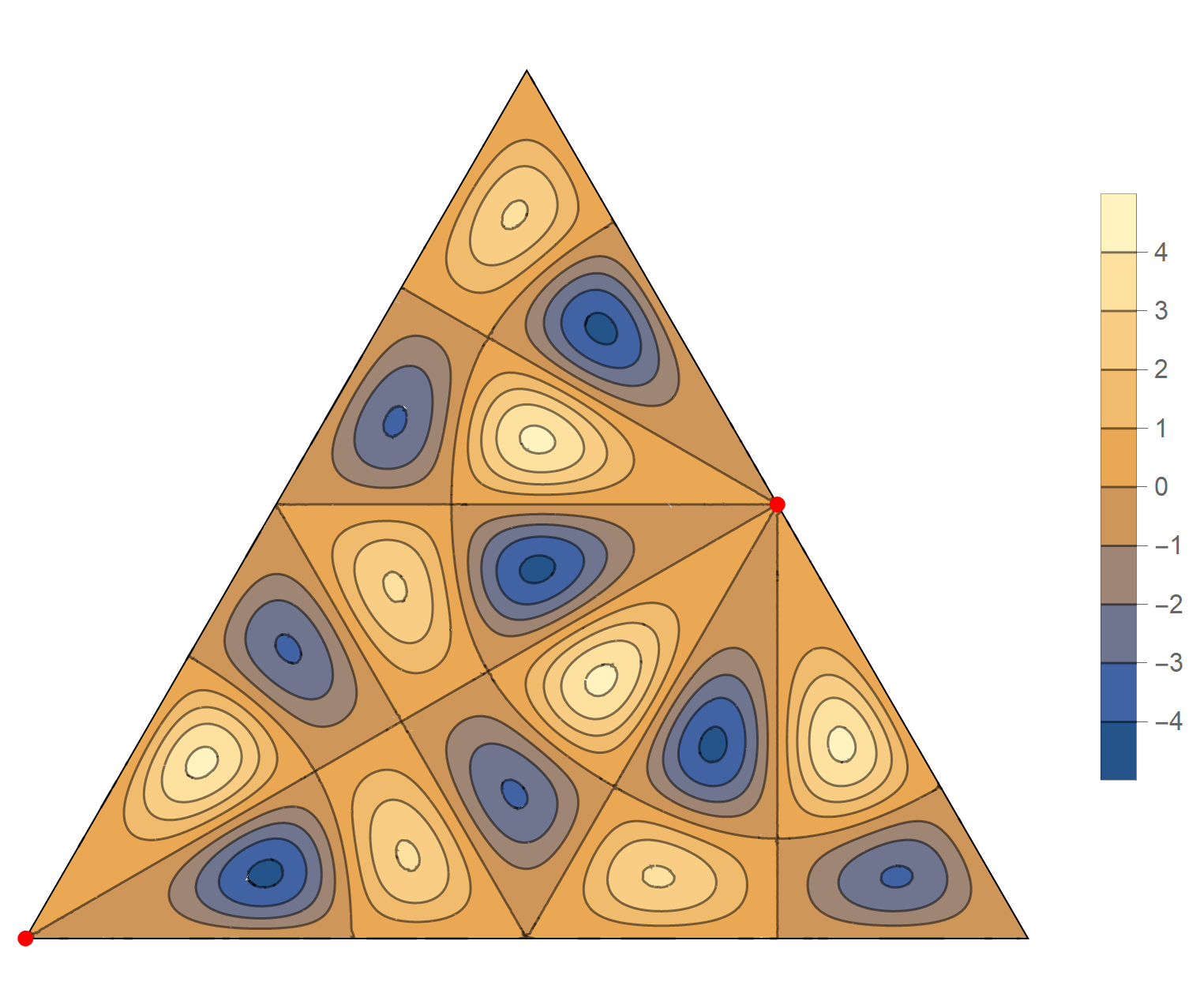
We review the entire two dimensional eigenspace as follows:
\[(\cos\theta)\operatorname{im}(x,y) +(\sin\theta) \operatorname{re}(x,y) \quad \text{as a function of} \quad \theta \in [0,2\pi).\]
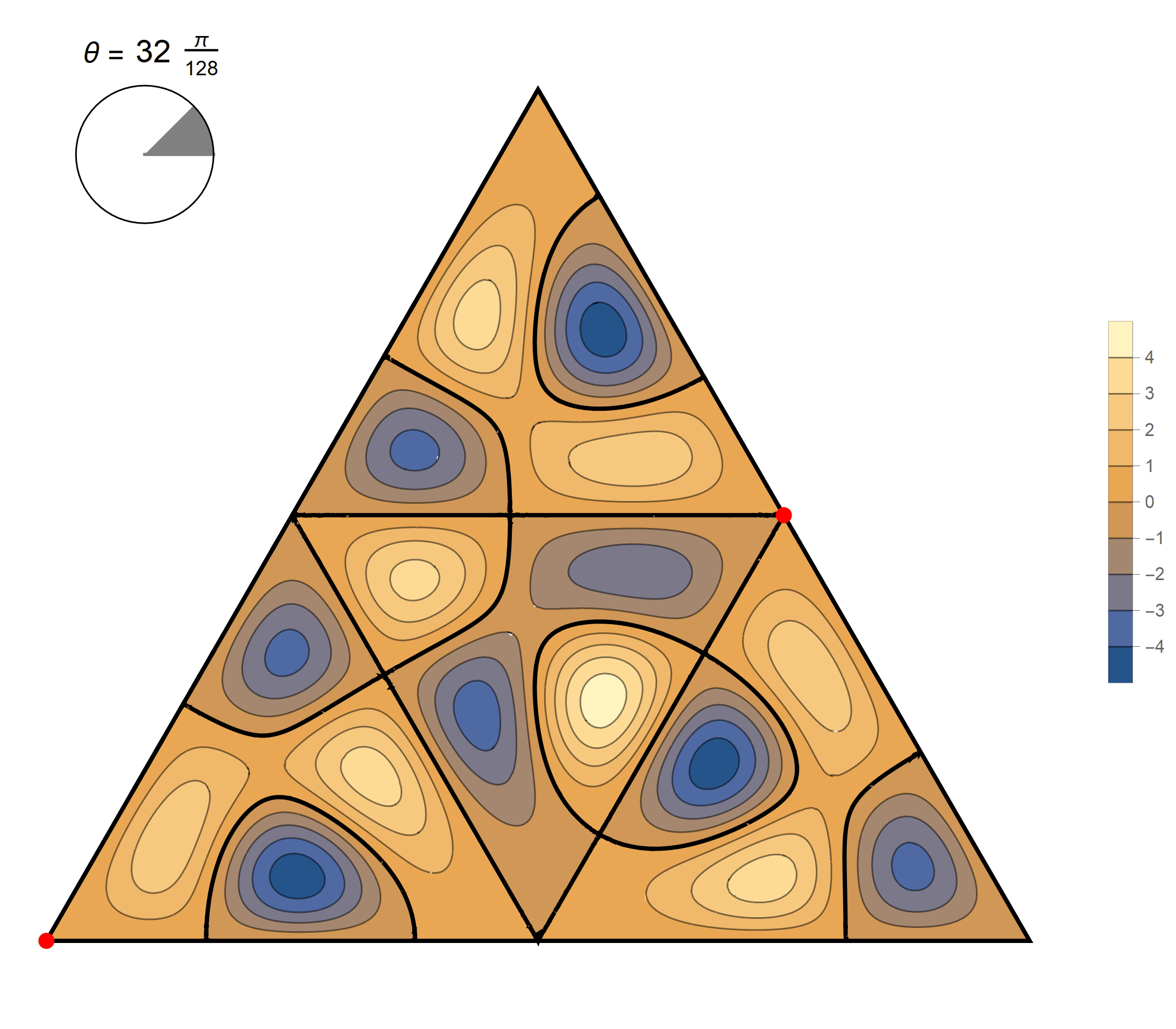
The sixteenth eigenvalue has multiplicity 2. The $(m,n)$ pairs that we used to construct the eigenfunction are \[ (9, 15), \quad (9, -6), \quad (-15, -6), \quad (-15, -9), \quad (6, -9), \quad (6, 15). \] The eigenfunctions are
\begin{align*} \operatorname{im}(x,y) & = -\sin \left(\frac{2}{3} \pi \left(6 x-8 \sqrt{3} y\right)\right)+\sin \left(\frac{2}{3} \pi \left(9 x-7 \sqrt{3} y\right)\right)+\sin \left(\frac{2}{3} \pi \left(-15 x-\sqrt{3} y\right)\right)\\ &\qquad\qquad-\sin \left(\frac{2}{3} \pi \left(\sqrt{3} y-15 x\right)\right)-\sin \left(\frac{2}{3} \pi \left(9 x+7 \sqrt{3} y\right)\right)+\sin \left(\frac{2}{3} \pi \left(6 x+8 \sqrt{3} y\right)\right) \\ \operatorname{re}(x,y) & =-\cos \left(\frac{2}{3} \pi \left(6 x-8 \sqrt{3} y\right)\right)+\cos \left(\frac{2}{3} \pi \left(9 x-7 \sqrt{3} y\right)\right)+\cos \left(\frac{2}{3} \pi \left(-15 x-\sqrt{3} y\right)\right)\\ &\qquad\qquad-\cos \left(\frac{2}{3} \pi \left(\sqrt{3} y-15 x\right)\right)-\cos \left(\frac{2}{3} \pi \left(9 x+7 \sqrt{3} y\right)\right)+\cos \left(\frac{2}{3} \pi \left(6 x+8 \sqrt{3} y\right)\right) \end{align*}
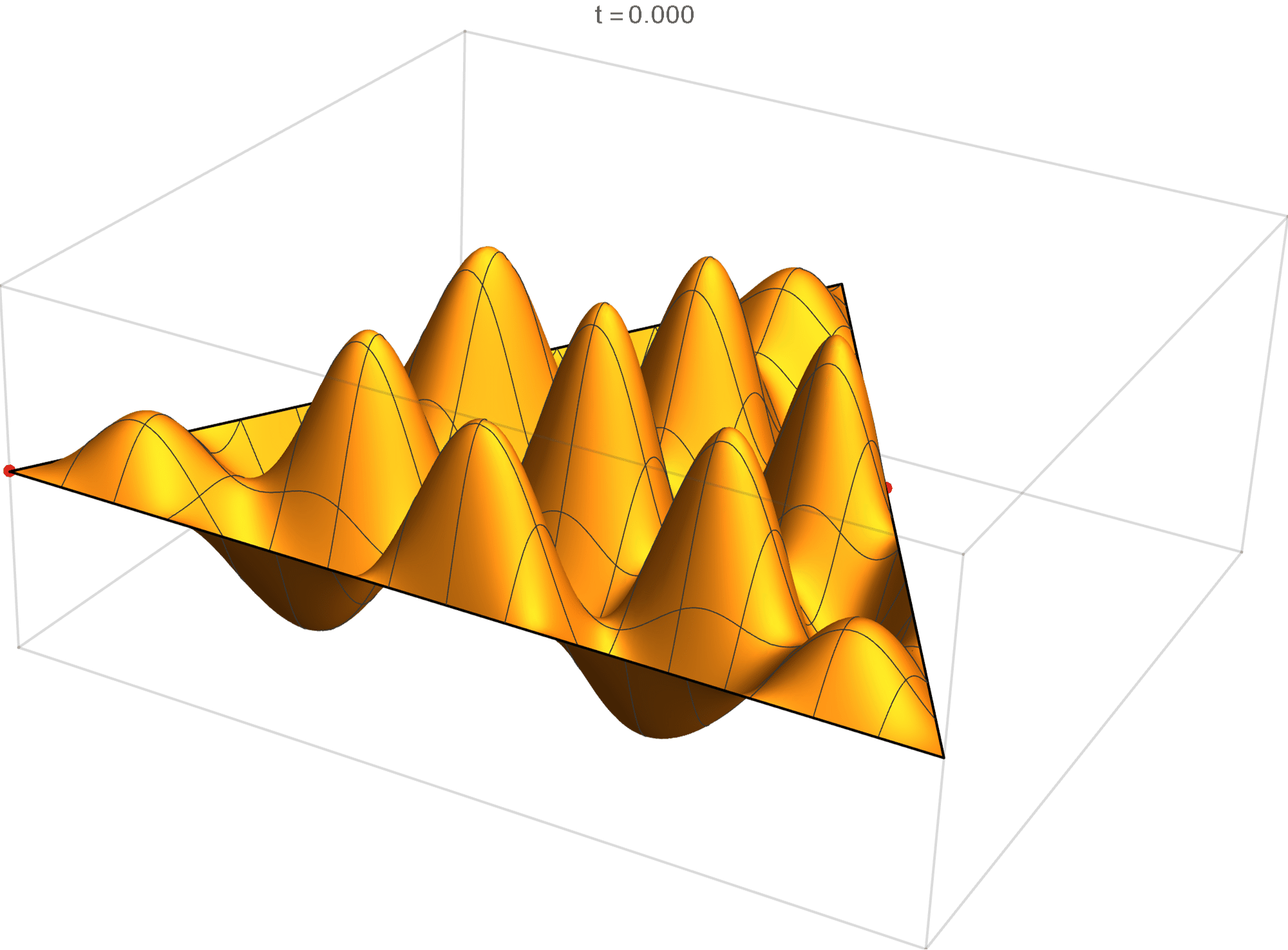
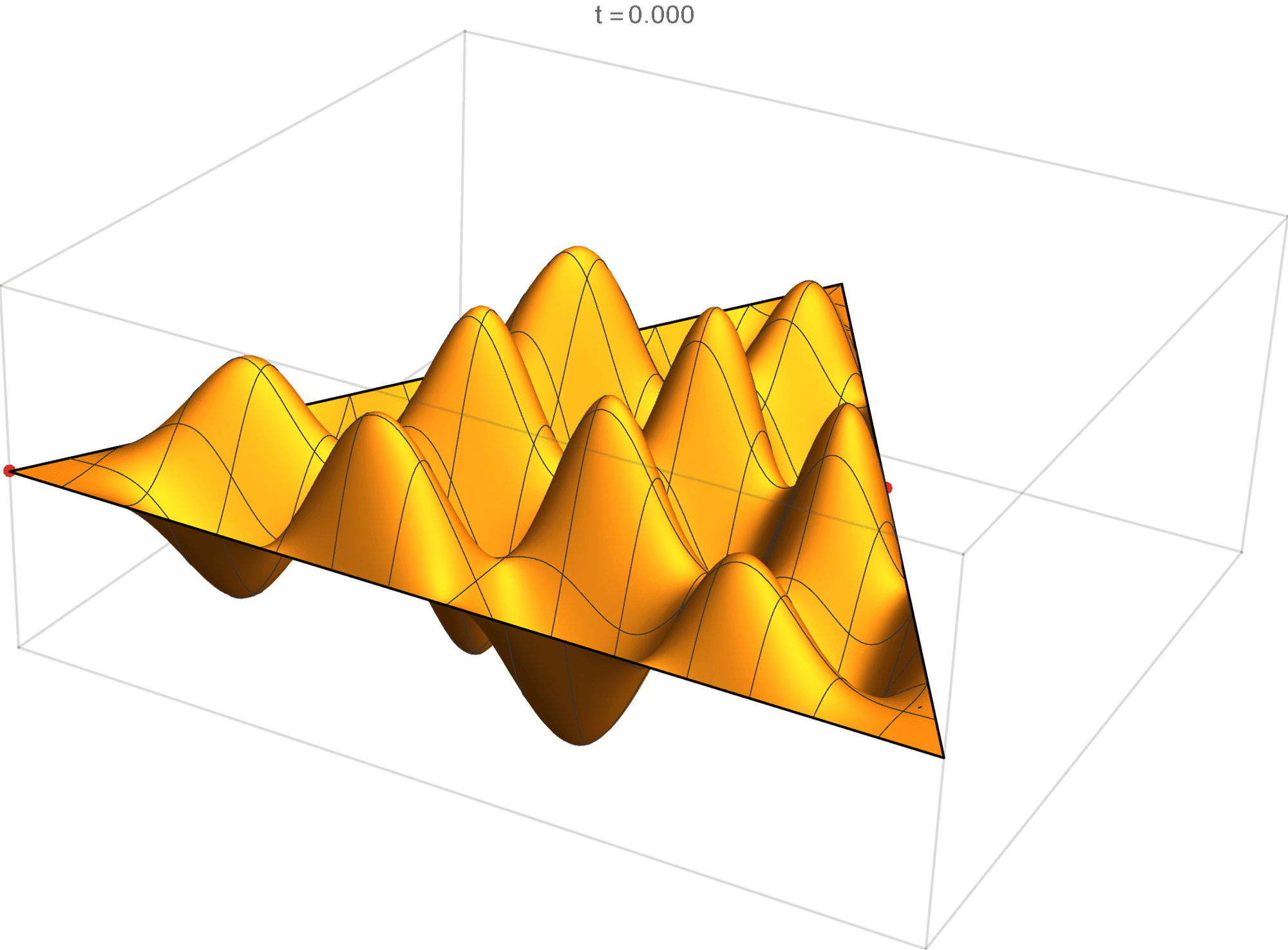
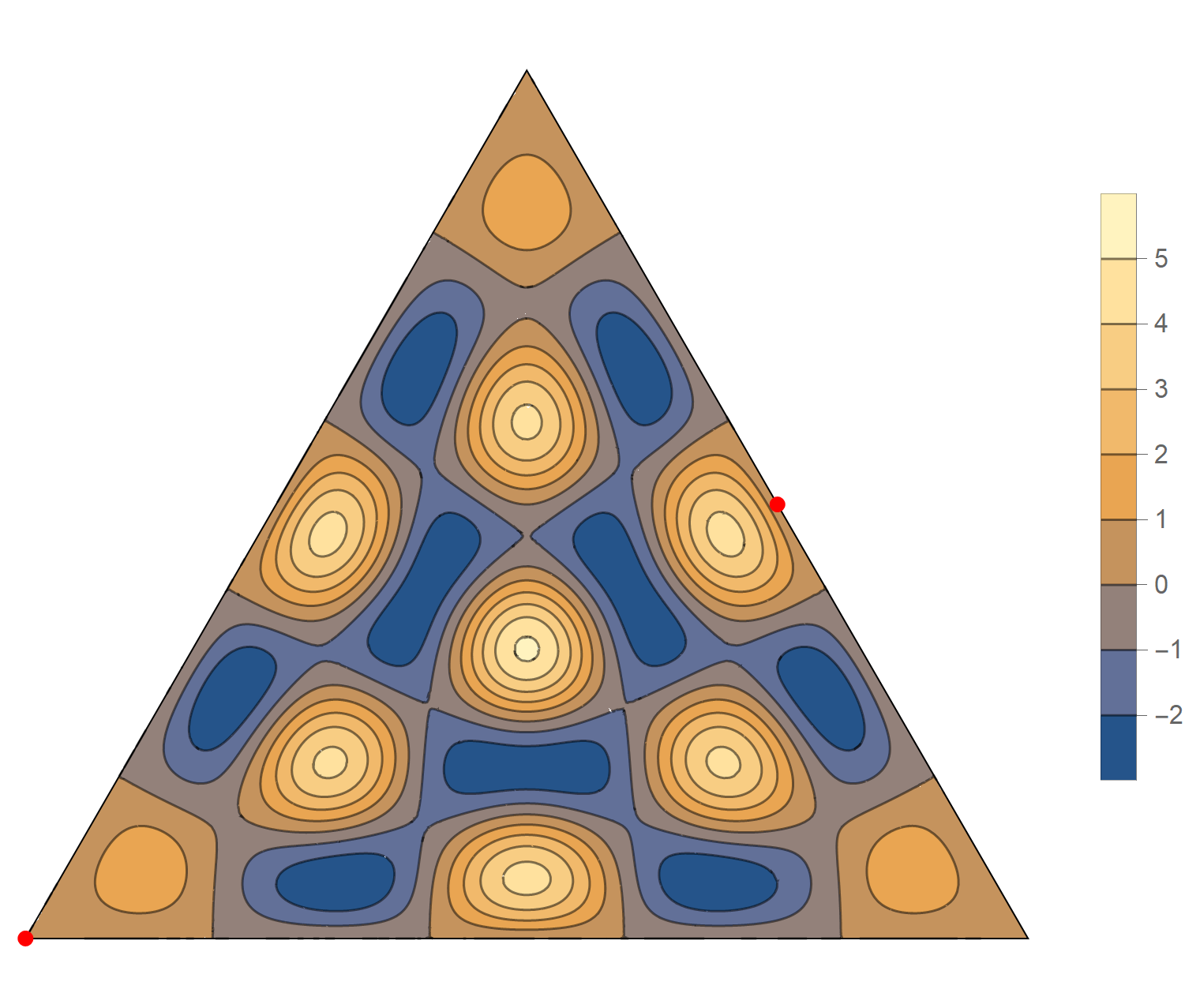
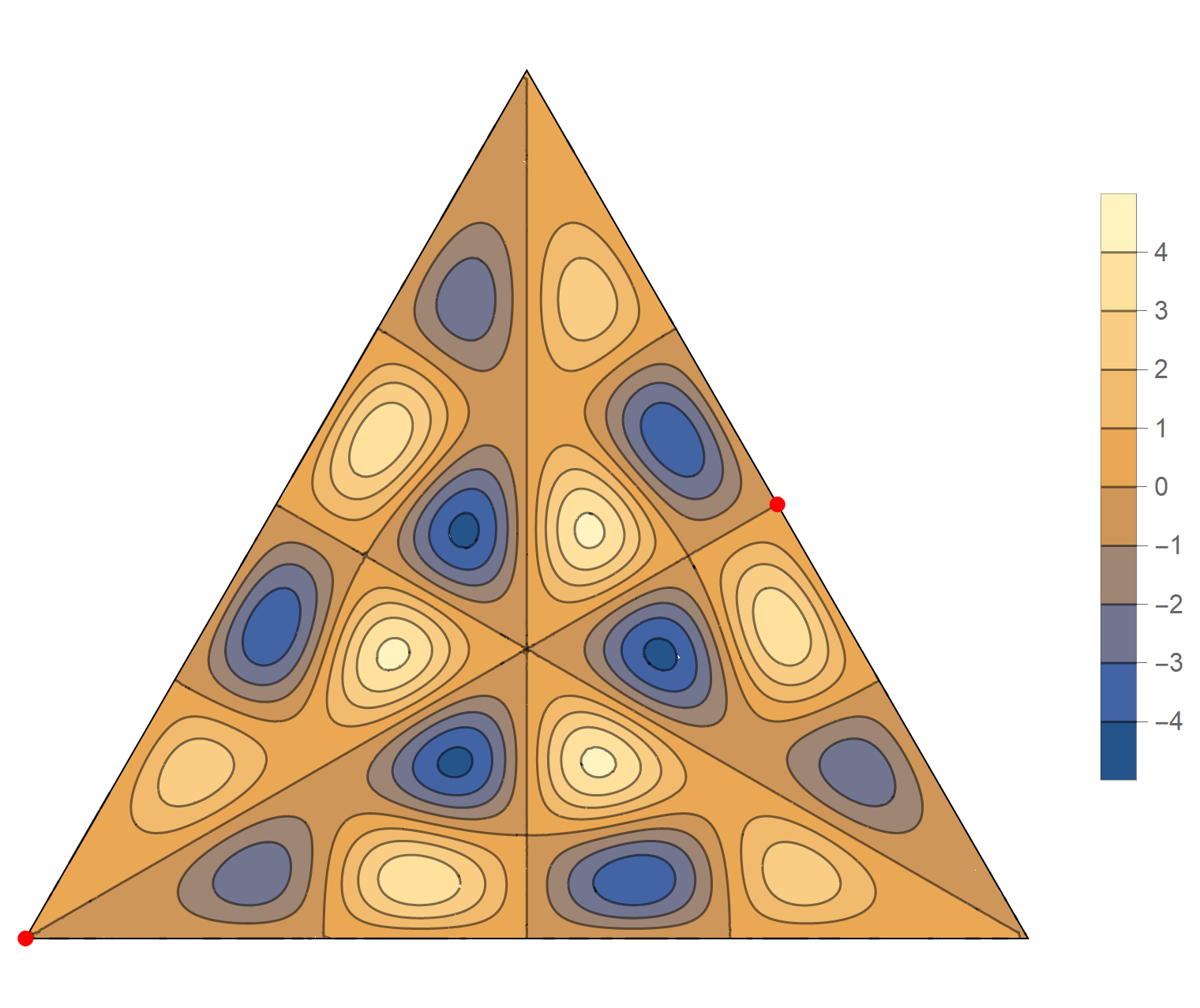
We review the entire two dimensional eigenspace as follows:
\[(\cos\theta)\operatorname{im}(x,y) +(\sin\theta) \operatorname{re}(x,y) \quad \text{as a function of} \quad \theta \in [0,2\pi).\]