Redshift
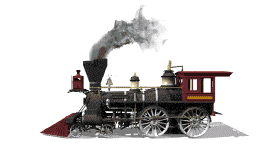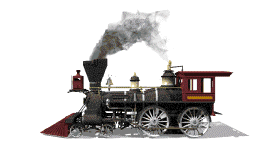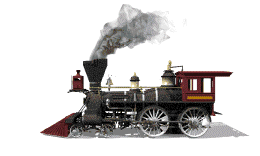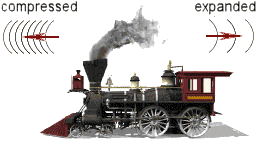 In 1842, Christian Doppler pointed out that an observed wavelength is
affected by the motion between the emitting source and the observer.
In 1842, Christian Doppler pointed out that an observed wavelength is
affected by the motion between the emitting source and the observer.
We've all witnessed the acoustical version of the effect. A train whistle or an ambulance siren sounds at a higher pitch as it approaches us, then the pitch sounds lower as it speeds past us. The effect is caused by a simple fact. In the direction of travel each successive wave is emitted closer to the preceding wave because the train has moved during the interval, thus compressing the overall frequency. Behind the train each successive wave is emmitted farther from the one just before it, expanding the frequency. In the same way, an approaching light source spectrum is seen as blueshifted as it approaches, and is redshifted when it moves away. We can use the shift to calculate how fast a light source, such as a star or galaxy, is moving towards us or away. The equation quantifying this effect when the velocity (v) of the light source is not too relativistic (less than 10% of light speed) is: 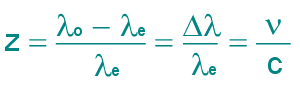
z is the shift. ν is the radial velocity between the source and observer. c is the velocity of light, 300,000 km/s. λo is the wavelength observed from the star and λe is the wavelength in the lab. If z is positive, the observer sees a redshift. Negative z indicates a blueshift (wavelengths are shortened) For example, the hydrogen alpha line has a laboratory wavelength of 656.285 nm. If this spectral line in the light from a nearby star is 656.315 nm, we can calculate the star's receding speed as follows: 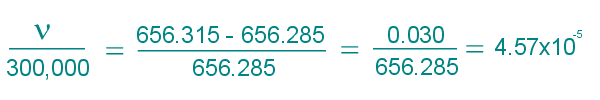
Therefore the star is moving away from us at 13.7 kilometers per second: 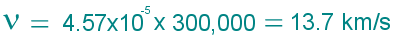
Redshift in Galaxies 
|