Coordinates
There are two primary ways to describe a position in the sky. One is the Horizon System,
also known as the Altitude-Azimuth System (Alt-Az). The other is the Equatorial System which uses coordinates
of Right Ascension and Declination (R.A. Dec).
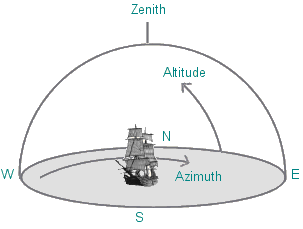
Horizon, or Altitude-Azimuth Coordinates This method is subjective, that is it describes positions from the observer's point of view. For example, when the Moon is half-way between the horizon and the zenith (straight up) from our point of view, we say it has an altitude of 45 degrees. When it is due south, we say it has an azimuth of 180 degrees (N=0, E=90, S=180, W=270). These two measurements describe the position: altitude 45 deg, azimuth 180 deg. A negative altitude describes objects below the horizon. Equatorial Coordinates Just as the latitude and longitude of a position on the Earth's surface define a unique location, regardless of the point of view, Right Ascension (R.A.) and Declination (Dec) of an object specify a unique position on the celestial sphere. For example, the star Sirius is always at R.A 6 hr 45 min (at least for our lifetime) and Dec. -16 degrees 43 minutes. Declination This is a measurement of degrees above or below the celestial equator. It ranges from -90 degrees at the south celestial pole to +90 degrees at the north celestial pole. 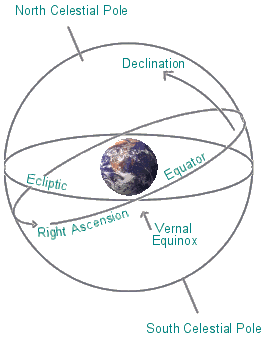 Right Ascension
Right AscensionThis is the hour angle measured along the celestial equator eastward from the node of the vernal equinox. It is measured in hours and minutes from 0 to 24 hours. The node of the equinox is the point where the Sun crosses the equator on its yearly trip northward in the spring. Sidereal Time This method of measuring time is related to Right Ascension because it is a clock that keeps track of the angle, measured in hours, minutes, and seconds, from the vernal equinox node to the observer's local meridian. The daily motion of this point provides a measure of the rotation of the Earth with respect to the stars, rather than the Sun. Therefore the sidereal clock runs faster than our regular clocks by about 4 minutes per day. To astronomers, Local Sidereal Time is useful because it corresponds to the coordinate of Right Ascension of celestial bodies that are presently on the local meridian. Put another way, the Right Ascension of a star is the hour, minute, and second it will cross your meridian, in sidereal time. |